数字电子技术中的异或门
在数字电子技术中,异或门是一种派生逻辑门,用于确定两个信号之间的差异。
在本章中,我们将研究异或门的理论和操作。让我们从异或门的基本定义开始。
什么是异或门?
异或门是数字电子技术中的一种逻辑门,具有两个输入和一个输出。只有当两个输入不同时,异或门的输出才为高电平或逻辑 1。对于相同的输入,异或门的输出为低电平或逻辑 0。
异或门也称为异或门或异或门。这种逻辑门广泛用于加法器和减法器等数字算术电路。
由于异或门的输出仅在两个输入不同时才为高,因此它也被称为不等式检测器。
需要注意的是,不存在三个或更多输入的异或门。因此,当我们需要用于两个以上输入变量的异或门时,我们会使用两个或更多个双输入异或门。
异或门的逻辑符号
异或门的逻辑符号如下图所示。

它只有两个输入,分别指定为A和B,一个输出,表示为Y。
异或门的真值表
异或门的真值表是表示其输入和输出之间关系的表格。
异或门的真值表如下所示 −
| 输入 | 输出 | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
从这个真值表中,我们可以观察到,仅当两个输入不同时,异或门的输出才为高电平或逻辑 1。在这种情况下,当两个输入相似时,输出为低或逻辑 0。
XOR 门的布尔表达式
布尔表达式是一个逻辑函数,它以数学方式表示 XOR 门的输入和输出之间的关系。
以下等式称为 XOR 门的布尔表达式。
$$\mathrm{Y \: = \: A \oplus B}$$
该等式也可以表示为以下 −
$$\mathrm{Y \: = \: AB' \: + \: A'B \: = \: A \bar{B} \: + \: \bar{A}B}$$
此处,符号"$\mathrm{\oplus}$"表示异或运算。
异或门的工作原理
异或门在不同输入组合下的详细工作原理如下 −
- 如果 A = 0 且 B = 0,则异或门的输出为 Y = 0。
- 如果 A = 0 且 B = 1,则异或门的输出为 Y = 1。
- 如果 A = 1 且 B = 0,则异或门的输出为 Y = 1。
- 如果 A = 1 且 B = 1,则异或门的输出为 Y = 0。
从这个解释中,我们可以看到异或门的输出仅当输入不同时才为高电平或逻辑 1。
XOR 门作为反相器
XOR 门也可用作反相器。XOR 运算有一个属性,即
$$\mathrm{A \: \oplus \: 1 \: = \: \bar{A}}$$
因此,利用此属性,我们可以说,如果 XOR 门的一条输入线连接到逻辑 1,并且输入信号应用于另一条输入线。然后,XOR 门产生所应用信号的反相版本作为输出。
下图显示了 XOR 门作为反相器的操作。
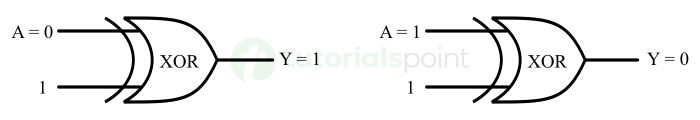
XOR 门作为缓冲器
缓冲门是一种产生与输入相同输出的逻辑门。它用于在输入和输出中提供一些延迟。
XOR 逻辑有一个属性,即,
$$\mathrm{A \: \oplus \: 0 \: = \: A}$$
因此,如果 XOR 门的两个输入线之一连接到逻辑 0,并且输入信号应用于另一条输入线。然后,XOR 门产生与输入相同的输出。
下图说明了 XOR 门作为缓冲逻辑的操作。
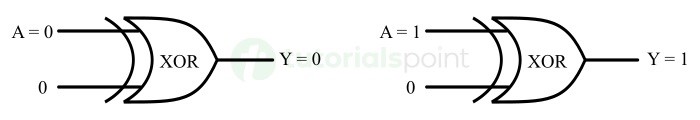
使用开关的 XOR 门
我们还可以使用电池、两个简单开关和一盏灯来实现 XOR 门逻辑。
下图描绘了使用开关的 XOR 门的电路图。
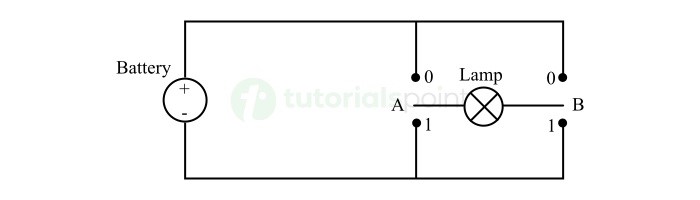
在此开关电路中,如果开关 A 和 B 处于同一电平(0 或 1),则灯不会发光。此状态表示低或逻辑 0 输出。
如果开关 A 和 B 处于不同的电平,即 A 为 0 而 B 为 1 或 A 为 1 而 B 为 0。那么,我们可以看到电流流过灯的路径是闭合的,从而使灯亮起。这表示高或逻辑 1 输出。
因此,上面显示的电路实现了 XOR 逻辑功能。
XOR 门的应用
以下是 XOR 门的一些关键应用 −
- XOR 门用于加法器、减法器等计算和算术电路。
- XOR 门用于检测两个逻辑电平或信号之间的错误、相似性和差异性。
- XOR 门用作受控反相器或缓冲逻辑。
结论
总之,XOR 门是一个双输入单输出逻辑门,当施加到它的输入不同时,它会产生高电平或逻辑 1 输出。
XOR 门逻辑广泛应用于楼梯电线和许多其他自动化电路,其中需要从两个不同位置控制单个设备(如灯)。


