什么是余3码?
余3码是一种非加权的BCD(二进制编码的十进制)码。它之所以被称为余3码,是因为它是由8421 BCD码加上0011(3)得到的。余3码也被称为XS-3,是一种将每个十进制数字表示为4位二进制码的BCD码。
余3二进制码是一种顺序码,因此我们可以使用它来执行算术运算。而且它是一种自补码,因此用补码法进行减法运算比8421 BCD码简单得多。
然而,余3码中有六个无效码,分别是0000、0001、0010、1110、1111。
如何得到余3码?
我们可以通过在自然的8421 BCD码上加上0011(3)来得到余3码。这里解释了 −
十进制数字 = 0 8421 BCD 码 = 0000 余 3 码 = 0000 + 0011 = 0011 十进制数字 = 1 8421 BCD 码 = 0001 余 3 码 = 0001 + 0011 = 0100
同样,我们可以得到所有十进制数字的余 3 码。
下表显示了每个十进制数字的余 3 码 −
| 十进制数字 | 余 3代碼 |
|---|---|
| 0 | 0011 |
| 1 | 0100 |
| 2 | 0101 |
| 3 | 0110 |
| 4 | 0111 |
| 5 | 1000 |
| 6 | 1001 |
| 7 | 1010 |
| 8 | 1011 |
| 9 | 1100 |
注意 − 如今,Excess-3 代码的使用并不广泛。它主要用于早期的数字系统。如今,许多其他先进而高效的二进制代码正在代替过剩 3 代码。
过剩 3 代码在数字电子技术中的重要性
过剩 3 代码是早期数字系统中广泛使用的二进制代码之一。以下是过剩 3 代码在数字电子技术领域使用的一些主要原因 −
- 它提供了一种将十进制数转换为二进制代码的简化方法。
- 它具有自补特性,使其适用于错误检测和纠正应用。
- 它是顺序代码,因此可用于在数字系统中执行算术运算。
- 过剩 3 代码与十进制 IO 设备高度兼容。因此,它为数字系统和其他设备之间提供了方便的接口。
余3码的优点
尽管余3码在现代数字系统中不太常见。但与其他二进制编码方案相比,它具有以下主要优势 −
- Excess-3 代码提供了一种以二进制形式表示十进制数的简单方法。
- Excess-3 代码提供了一种无需使用任何复杂转换方法即可执行加法和减法运算的更简单方法。
- Excess-3 代码很容易转换为十进制数或从十进制数转换为十进制数。
- Excess-3 代码是二进制编码的十进制数,与各种十进制设备高度兼容。
Excess-3 代码的缺点
Excess-3 代码有几个优点,但也有一些缺点,这就是它在现代数字系统中不太常用的原因。以下是余 3 码的一些主要缺点 −
- 与纯二进制相比,余 3 码是一种低效的十进制数二进制表示。这是因为它需要更多位来表示十进制数字。
- 余 3 码需要额外的算术电路才能将 3 添加到标准二进制代码中。
- 余 3 码与纯二进制系统的兼容性有限。
余 3 码的应用
余 3 码在早期的数字系统和数字计算机中得到广泛应用。余 3 码应用的关键领域如下 −
- 余 3 码用于早期的数字计算机。
- 余 3 码也用于通过数字系统进行十进制数据处理。
- 余 3 码也用于使用十进制数据的数字设备,如打印机、读卡器等。
- 余 3 码的自补特性使其适合用于错误检测和纠正应用。
- 余 3 码也用于通信和数据传输应用。
余 3 加法
在余 3 加法中,从 LSD(最低有效位)开始,我们在每列中添加 4 位组。
如果 4 位组的加法没有产生循环进位,我们必须从和项中减去 0011得到结果。这是因为,没有进位意味着结果是XS-6格式。因此,我们通过在和项中添加0011来获得正确的和。
如果加法产生了循环进位,我们必须在和项中添加0011才能得到正确的结果。这是因为进位表示和项是一个无效的超3代码,通过在和项中添加0011来纠正。
让我们借助例子来理解XS-3加法。
示例
在 XS-3 代码中将 35 和 28 相加。
解决方案
给定的十进制数及其 XS-3 代码为
35 = 0110 1000
28 = 0101 1011
添加 XS-3 代码,
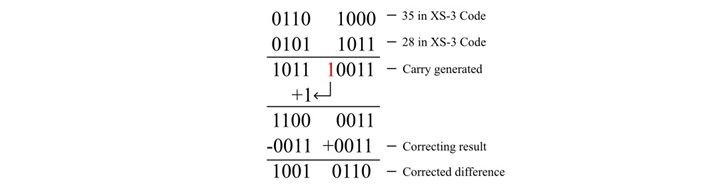
因此,35 和 28 的正确总和在 XS-3 中为 1001 0110,在十进制中为 63。
Excess-3减法
在 XS-3 减法中,从最低有效数字开始,我们通过从被减数的相应 4 位组中减去减数的每组 4 位来找到两个数字之间的差值。
在 XS-3 减法中,如果没有从较高的 4 位组中借位,那么我们将 0011 添加到差值项中以获得更正的结果。这是因为,如果没有借位,则结果为普通二进制,必须通过向其添加 0011 将其转换为 XS-3。
如果从下一个 4 位组中借位,则差分项将是无效的 XS-3 代码,通过从中减去 0011 进行更正。
让我们通过一个已解决的示例来理解 XS-3 减法。
示例
在 XS-3 代码中从 56 中减去 28。
解决方案
已知,
被减数 = (56)10 = (1000 1001)XS-3
减数 = (28)10 = (0101 1011)XS-3
在 XS-3 代码中减去,我们得到,

因此,56 和 28 的修正差在 XS-3 代码中为 0101 1011,在十进制中为 28。
结论
总之,Excess-3 (XS-3) 代码是一种广泛用于旧数字系统的二进制编码方案。它基本上是一种 BCD 方案,用于以二进制格式表示十进制数字。
在现代数字系统中,多余的 3 码被更高效的二进制代码所取代,例如 8421 BCD 码、ASCII 码等。


