数字电子技术 - 触发器的转换
在上一章中,我们讨论了四种触发器,即 SR 触发器、D 触发器、JK 触发器和 T 触发器。我们可以通过添加一些额外的逻辑将一个触发器转换为其余三个触发器。因此,总共会有十二个触发器转换。
按照这些步骤将一个触发器转换为另一个触发器。
- 考虑所需触发器的特性表。
- 为当前状态和下一个状态的每个组合填写给定触发器的激励值(输入)。所有触发器的激励表如下所示。
| 当前状态 | 下一状态 | SR 触发器输入 | D 触发器输入 | JK 触发器输入 | T 触发器输入 | ||
|---|---|---|---|---|---|---|---|
| Q(t) | Q(t+1) | S | R | D | J | K | T |
| 0 | 0 | 0 | x | 0 | 0 | x | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | x | 1 |
| 1 | 0 | 0 | 1 | 0 | x | 1 | 1 |
| 1 | 1 | x | 0 | 1 | x | 0 | 0 |
获取每个激励输入的简化表达式。如有必要,使用 Kmaps 进行简化。
根据简化表达式,使用给定的触发器和必要的逻辑门绘制所需触发器的电路图。
现在,让我们将一些触发器转换为其他触发器。其余触发器转换请按照相同流程进行。
SR 触发器到其他触发器的转换
以下是 SR 触发器到其他触发器的三种可能转换。
- SR 触发器到 D 触发器
- SR 触发器到 JK 触发器
- SR 触发器到 T 触发器
SR 触发器到 D 触发器的转换
此处,给定的触发器是 SR 触发器,而所需的触发器是 D 触发器。因此,请考虑以下 D 触发器的特性表。
| D 触发器输入 | 当前状态 | 下一状态 |
|---|---|---|
| D | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
我们知道 SR 触发器有两个输入 S 和 R。因此,请写下当前状态和下一状态值的每个组合的 SR 触发器的激励值。下表显示了 D 触发器的特性表以及 SR 触发器的激励输入。
| D 触发器输入 | 当前状态 | 下一状态 | SR 触发器输入 | |
|---|---|---|---|---|
| D | Q(t) | Q(t + 1) | S | R |
| 0 | 0 | 0 | 0 | x |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | x | 0 |
从上表中,我们可以为每个输入编写如下的布尔函数。
$$\mathrm{S \: = \: m_{2} \: + \: d_{3}}$$
$$\mathrm{R \: = \: m_{1} \: + \: d_{0}}$$
我们可以使用 2 个变量 K-Maps 来获取这些输入的简化表达式。S 和 R 的 k-Maps 如下所示。
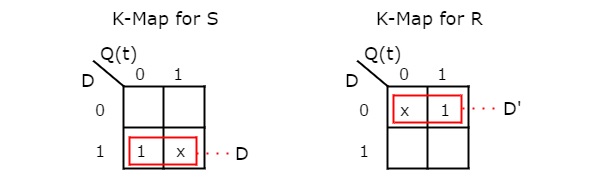
因此,我们得到 S = D &简化后,R = D'。D 触发器的电路图如下图所示。
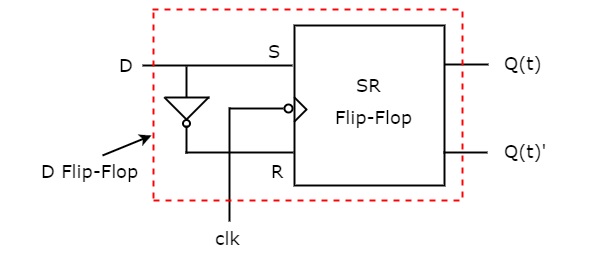
该电路由 SR 触发器和一个反相器组成。该反相器产生的输出是输入 D 的补码。因此,整个电路具有单个输入 D 和两个输出 Q(t) 和 Q(t)'。因此,它是一个 D 触发器。类似地,您可以进行其他两种转换。
D 触发器到其他触发器的转换
以下是 D 触发器到其他触发器的三种可能转换。
- D 触发器到 T 触发器
- D 触发器到 SR 触发器
- D 触发器到 JK 触发器
D 触发器到 T 触发器的转换
这里,给定的触发器是 D 触发器,所需的触发器是 T 触发器。因此,请考虑以下 T 触发器的特性表。
| T 触发器输入 | 当前状态 | 下一状态 |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
我们知道 D 触发器只有一个输入 D。因此,请写下 D 触发器对当前状态和下一状态值的每个组合的激励值。下表显示了 T 触发器的特性表以及 D 触发器的激励输入。
| T 触发器输入 | 当前状态 | 下一状态 | D 触发器输入 |
|---|---|---|---|
| T | Q(t) | Q(t + 1) | D |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
从上表中,我们可以直接写出 D 的 布尔函数,如下所示。
$$\mathrm{D \: = \: T \: \oplus \: Q \: \left ( t \: \right )}$$
因此,我们需要一个双输入异或门以及 D 触发器。T 触发器的电路图如下图所示。
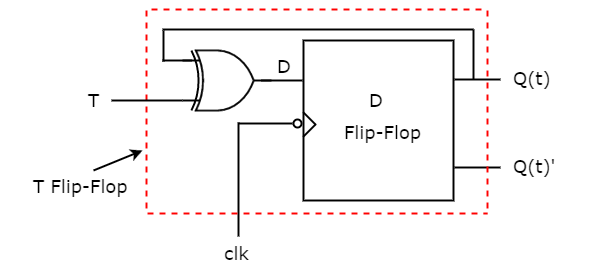
该电路由 D 触发器和一个异或门组成。该异或门产生一个输出,它是 T 和 Q(t) 的异或。因此,整个电路具有单个输入 T 和两个输出 Q(t) 和 Q(t)'。因此,它是一个 T 触发器。类似地,您可以进行其他两种转换。
JK触发器到其他触发器的转换
以下是JK触发器到其他触发器的三种可能转换。
- JK触发器到T触发器
- JK触发器到D触发器
- JK触发器到SR触发器
JK触发器到T触发器的转换
这里,给定的触发器是JK触发器,所需的触发器是T触发器。因此,请考虑以下 T 触发器的特性表。
| T 触发器输入 | 当前状态 | 下一状态 |
|---|---|---|
| T | Q(t) | Q(t + 1) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
我们知道 JK 触发器有两个输入 J 和 K。因此,请写下 JK 触发器的当前状态和下一状态值的每个组合的激励值。下表显示了 T 触发器的特性表以及 JK 触发器的激励输入。
| T 触发器输入 | 当前状态 | 下一状态 | JK 触发器输入 | |
|---|---|---|---|---|
| T | Q(t) | Q(t + 1) | J | K |
| 0 | 0 | 0 | 0 | x |
| 0 | 1 | 1 | x | 0 |
| 1 | 0 | 1 | 1 | x |
| 1 | 1 | 0 | x | 1 |
从上表中,我们可以为每个输入编写布尔函数,如下所示。
$$\mathrm{J \: = \: m_{2} \: + \: d_{1} \: + \: d_{3}}$$
$$\mathrm{K \: = \: m_{3} \: + \: d_{0} \: + \: d_{2}}$$
我们可以使用 2 个变量 K-Maps 来获取这两个输入的简化表达式。J 和 的 k-Maps K 如下所示。
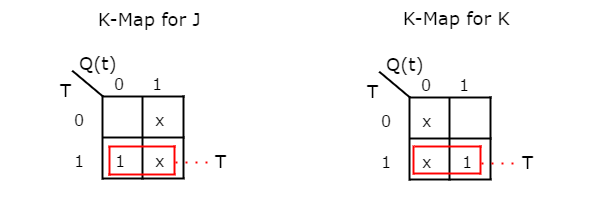
因此,经过简化,我们得到 J = T & K = T。T 触发器的电路图如下图所示。
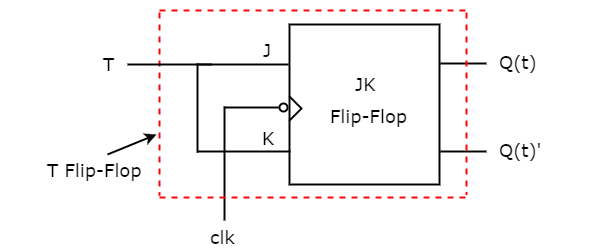
该电路仅由 JK 触发器组成。它不需要任何其他门。只需将相同的输入 T 连接到 J 和 K。因此,整个电路具有单个输入 T 和两个输出 Q(t) 和 Q(t)'。因此,它是一个 T 触发器。类似地,您可以进行其他两种转换。
T 触发器到其他触发器的转换
以下是 T 触发器到其他触发器的三种可能转换。
- T 触发器到 D 触发器
- T 触发器到 SR 触发器
- T 触发器到 JK 触发器
T 触发器到 D 触发器的转换
这里,给定的触发器是 T 触发器,而所需的触发器是 D 触发器。因此,考虑 D 触发器的特性表,并写下当前状态和下一状态值的每个组合的 T 触发器的激励值。下表显示了 D 触发器的特性表以及 T 触发器的激励输入。
| D 触发器输入 | 当前状态 | 下一状态 | T 触发器输入 | |
|---|---|---|---|---|
| D | Q(t) | Q(t + 1) | T | |
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | |
从上表中,我们可以直接写出 T 的布尔函数,如下所示。
$$\mathrm{T \: = \: D \: \oplus \: Q \left ( t \right )}$$
因此,我们需要一个双输入异或门和 T 触发器。D 触发器的电路图如下图所示。
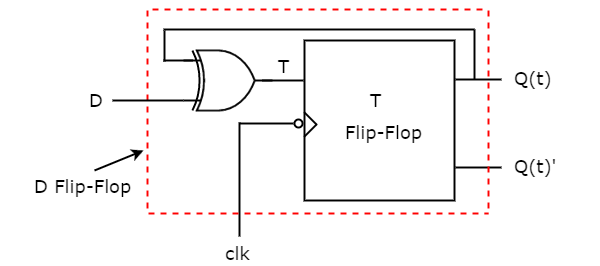
该电路由 T 触发器和一个异或门组成。该异或门产生一个输出,它是 D 和 Q(t) 的异或。因此,整个电路具有单个输入 D 和两个输出 Q(t) & Q(t)'。因此,它是一个D触发器。类似地,您可以进行另外两个转换。


