数字电子技术 - 解码器
什么是解码器?
在数字电子技术中,将 N 位二进制输入代码转换为 M 个输出通道的组合逻辑电路称为 解码器,该电路对于每个可能的输入组合仅激活一个输出通道。
换句话说,将 N 条输入线转换为最多 2N 条输出线的组合逻辑电路称为 解码器。
因此,解码器是一种能够识别或检测特定代码的组合逻辑电路。解码器执行的操作称为解码。图 1 显示了解码器的一般框图。
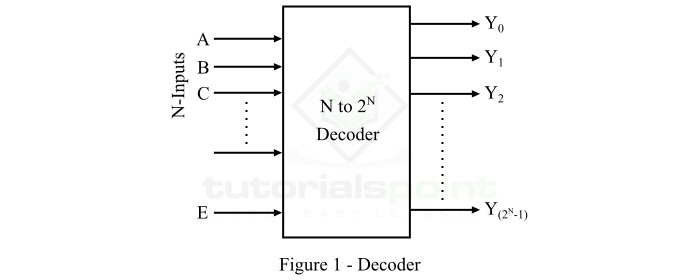
此处,解码器有 N 条输入线和 M (2N) 条输出线。在解码器中,N 条输入线中的每一条都可以是 0 或 1,因此可能的输入组合或代码的数量等于 2N。对于这些输入组合中的每一种,M 条输出线中只有一条是活动的,而所有其他输出线将保持非活动状态。
解码器的类型
目前有几种类型的解码器。但是,根据存在的输入和输出线,解码器可分为以下三种类型 −
- 2 到 4 解码器
- 3 到 8 解码器
- 4 到 16 解码器
现在,让我们逐一详细讨论每种类型的解码器。
2 到 4 解码器
2 到 4 解码器具有 2 条输入线和 4 条(22)输出线。 2 至 4 解码器的功能框图如图 2 所示。

当借助启用输入 E 启用此解码器时,其四个输出中的一个将针对每个输入组合处于活动状态。可以借助下面给出的真值表来分析此 2 线至 4 线解码器的操作。
| 输入 | 输出 | |||||
|---|---|---|---|---|---|---|
| E | A | B | Y3 | Y2 | Y1 | Y0 |
| 0 | X | X | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
使用此真值表,我们可以得出每个输出的布尔表达式如下 −
$$\mathrm{Y_{0} \: = \: E \: \cdot \: \bar{A} \: \cdot \: \bar{B}}$$
$$\mathrm{Y_{1} \: = \: E \: \cdot \: \bar{A} \: \cdot \: B}$$
$$\mathrm{Y_{2} \: = \: E \: \cdot \: A \: \cdot \: \bar{B}}$$
$$\mathrm{Y_{3} \: = \: E \: \cdot \: A \: \cdot \: B}$$
由于每个输出项都包含输入变量的乘积,因此可以借助与门来实现。因此,2 至 4 解码器的逻辑电路图如图 3 所示。

操作
2 至 4 解码器的逻辑电路操作如下 −
- 当使能输入 (E) 处于非活动状态,即设置为 0 时,所有与门均不起作用。
- 当使能输入 (E) 设置为 1 时,电路将按如下所述工作。
- 当 A = 0 且 B = 0 时,与门 1 变为活动状态并产生输出 Y0。
- 当 A = 0 且 B = 1 时,与门 2 变为活动状态并产生输出Y1。
- 当 A = 1 且 B = 0 时,AND 门 3 变为活动状态并产生输出 Y2。
- 当 A = 1 且 B = 1 时,AND 门 4 变为活动状态并产生输出 Y3。
3 到 8 解码器
3 到 8 解码器具有 3 条输入线和 8 条 (23) 输出线。3 到 8 解码器的功能框图如图 4 所示。
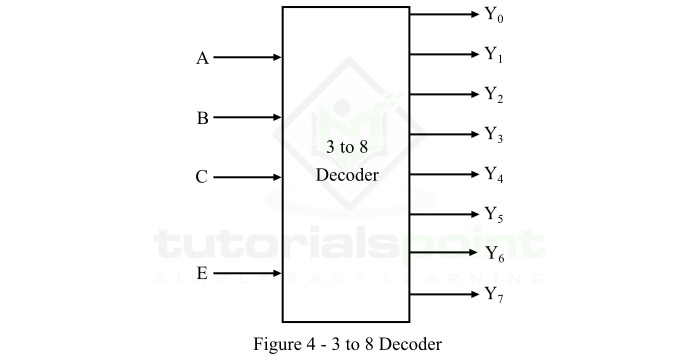
当借助启用输入 E 启用此解码器时,对于每个输入组合,它的八个输出之一将处于活动状态。可以借助下面给出的功能表来分析此 3 线到 8 线解码器的操作。
| 输入 | 输出 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| E | A | B | C | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
| 0 | X | X | X | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
使用此函数表,我们可以得出每个输出的布尔表达式如下 −
$$\mathrm{Y_{0} \: = \: E \: \bar{A} \: \bar{B} \: \bar{C}}$$
$$\mathrm{Y_{1} \: = \: E \: \bar{A} \: \bar{B} \: C}$$
$$\mathrm{Y_{2} \: = \: E \: \bar{A} \: B \: \bar{C}}$$
$$\mathrm{Y_{3} \: = \: E \: \bar{A} \: B \: C}$$
$$\mathrm{Y_{4} \: = \: E \: A \: \bar{B} \: \bar{C}}$$
$$\mathrm{Y_{5} \: = \: E \: A \: \bar{B} \: C}$$
$$\mathrm{Y_{6} \: = \: E \: A \: B \: \bar{C}}$$
$$\mathrm{Y_{7} \: = \: E \: A \: B \: C}$$
我们可以看到,每个输出项都包含输入变量的乘积,因此它们可以借助与门来实现。因此,3 至 8 解码器的逻辑电路图如图 5 所示。
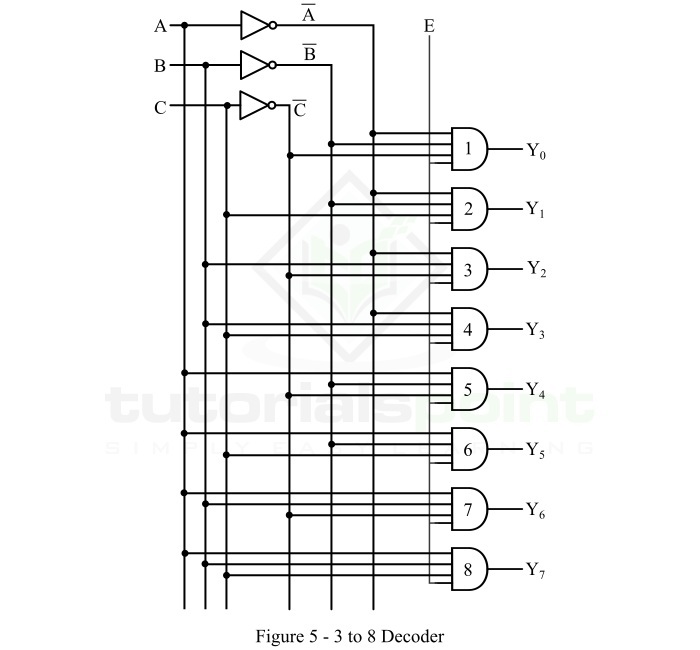
操作
3 至 8 解码器的逻辑电路操作如下 −
- 当使能输入 (E) 处于非活动状态,即设置为 0 时,所有与门均不起作用。
- 当使能输入 (E) 设置为 1 使其处于活动状态时,电路将按如下所述工作。
- 当 A = 0、B = 0 和 C = 0 时,与门 1 变为活动状态并产生输出 Y0。
- 当 A = 0、B = 0 和 C = 1 时,与门 2 变为有效并产生输出 Y1。
- 当 A = 0、B = 1 且 C = 0 时,与门 3 变为有效并产生输出 Y2。
- 当 A = 0、B = 1 且 C = 1 时,与门 4 变为有效并产生输出 Y3。
- 当 A = 1、B = 0 且 C = 0 时,与门 5 变为有效并产生输出 Y4。
- 当 A = 1、B = 0 且 C = 1 时,与门 6 变为有效并产生输出 Y5。
- 当 A = 1、B = 1 且 C = 0 时,与门 7 变为有效并产生输出 Y6。
- 当 A = 1 时, B = 1,且 C = 1,AND 门 8 变为活动状态并产生输出 Y7。
4 至 16 解码器
4 至 16 解码器是一种具有 4 条输入线和 16 条(214)输出线的解码器。4 至 16 解码器的功能框图如图 6 所示。
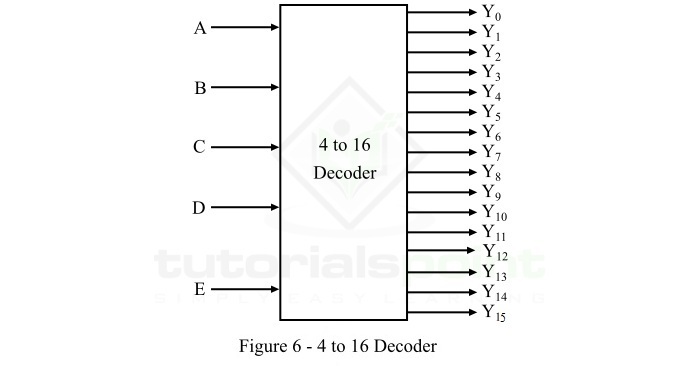
当借助启用输入 E 启用此解码器时,对于每种输入组合,它的十六个输出之一将处于活动状态。可以借助下面给出的功能表分析 4 线至 16 线解码器的操作。
| 输入 | 输出 | ||||
|---|---|---|---|---|---|
| E | A | B | C | D | |
| 0 | X | X | X | X | 0 |
| 1 | 0 | 0 | 0 | 0 | Y0 |
| 1 | 0 | 0 | 0 | 1 | Y1 |
| 1 | 0 | 0 | 1 | 0 | Y2 |
| 1 | 0 | 0 | 1 | 1 | Y3 |
| 1 | 0 | 1 | 0 | 0 | Y4 |
| 1 | 0 | 1 | 0 | 1 | Y5 |
| 1 | 0 | 1 | 1 | 0 | Y6 |
| 1 | 0 | 1 | 1 | 1 | Y7 |
| 1 | 1 | 0 | 0 | 0 | Y8 |
| 1 | 1 | 0 | 0 | 1 | Y9 |
| 1 | 1 | 0 | 1 | 0 | Y10 |
| 1 | 1 | 0 | 1 | 1 | Y11 |
| 1 | 1 | 1 | 0 | 0 | Y12 |
| 1 | 1 | 1 | 0 | 1 | Y13 |
| 1 | 1 | 1 | 1 | 0 | Y14 |
| 1 | 1 | 1 | 1 | 1 | Y15 |
从该函数表中,我们可以直接为每个输出写出布尔表达式,如下所示 −
$$\mathrm{Y_{0} \: = \: E \: \bar{A} \: \bar{B} \: \bar{C} \: \bar{D}}$$
$$\mathrm{Y_{1} \: = \: E \: \bar{A} \: \bar{B} \: \bar{C} \: D}$$
$$\mathrm{Y_{2} \: = \: E \: \bar{A} \: \bar{B} \: C \: \bar{D}}$$
$$\mathrm{Y_{3} \: = \: E \: \bar{A} \: \bar{B} \: C \: D}$$
$$\mathrm{Y_{4} \: = \: E \: \bar{A} \: B \: \bar{C} \: \bar{D}}$$
$$\mathrm{Y_{5} \: = \: E \: \bar{A} \: B \: \bar{C} \: D}$$
$$\mathrm{Y_{6} \: = \: E \: \bar{A} \: B \: C \: \bar{D}}$$
$$\mathrm{Y_{7} \: = \: E \: \bar{A} \: B \: C \: D}$$
$$\mathrm{Y_{8} \: = \: E \: A \: \bar{B} \: \bar{C} \: \bar{D}}$$
$$\mathrm{Y_{9} \: = \: E \: A \: \bar{B} \: \bar{C} \: D}$$
$$\mathrm{Y_{10} \: = \: E \: A \: \bar{B} \: C \: \bar{D}}$$
$$\mathrm{Y_{11} \: = \: E \: A \: \bar{B} \: C \: D}$$
$$\mathrm{Y_{12} \: = \: E \: A \: B \: \bar{C} \: \bar{D}}$$
$$\mathrm{Y_{13} \: = \: E \: A \: B \: \bar{C} \: D}$$
$$\mathrm{Y_{14} \: = \: E \: A \: B \: C \: \bar{D}}$$
$$\mathrm{Y_{15} \: = \: E \: A \: B \: C \: D}$$
我们可以采用与 2 到 4 解码器和 3 到 8 解码器相同的方式实现这些输出表达式。
现在,让我们讨论解码器的应用。
解码器的应用
解码器用于仅在出现特定输入代码组合时激活输出或输出集合的情况。下面列出了解码器的一些重要应用 −
- 解码器用于代码转换。
- 解码器广泛用于计算机的存储系统。
- 解码器还用于解复用或数据分发。
- 解码器还用于需要非常短的传播延迟的数据路由应用。
- 解码器还可用于定时或排序目的。
- 解码器还用于在特定时间打开和关闭数字设备。
这就是解码器及其在数字电子系统中的应用。


