二进制到格雷码转换器
二进制到格雷码转换器是一种可以将二进制代码转换为其等效格雷码的代码转换器。
二进制到格雷码转换器接受二进制数作为输入,并产生相应的格雷码作为输出。
以下是真值表,解释了 4 位二进制到格雷码转换器的操作。
| 二进制代码 | 格雷码 | ||||||
|---|---|---|---|---|---|---|---|
| B3 | B2 | B1 | B0 | G3 | G2 | G1 | G0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
让我们推导出格雷码输出位的布尔表达式。为此,我们将使用 K-map 技术简化真值表。
格雷码位 G0 的 K-Map>
下图显示了用于获得格雷码位 G0 的布尔表达式的 K-Map 简化。
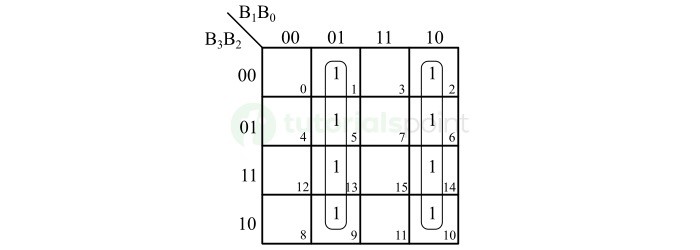
因此,格雷码位 G0 的布尔表达式为,
$$\mathrm{G_{0} \: = \: \overline{B_{1}} \: B_{0} \: + \ B_{1} \: \overline{B_{0}} \: = \: B_{0} \: \oplus \: B_{1}}$$
格雷码位 G1 的 K-Map>
格雷码位 G1 的 K-Map 简化如下所示 −
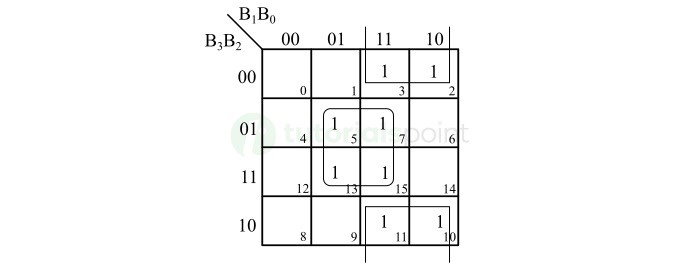
因此,格雷码位 G1 的布尔表达式为,
$$\mathrm{G_{1} \: = \: \overline{B_{2}} \: B_{1} \: + \ B_{2} \: \overline{B_{1}} \: = \: B_{1} \: \oplus \: B_{2}}$$
格雷码位 G2 的 K-Map>
格雷码位 G2 的 K-Map 简化如下图所示 −
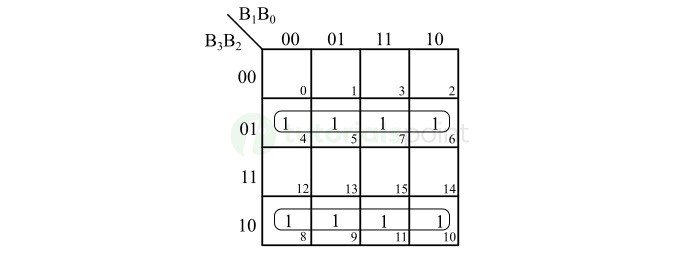
格雷码位 G2 的布尔表达式为,
$$\mathrm{G_{2} \: = \: \overline{B_{3}} \: B_{2} \: + \ B_{3} \: \overline{B_{2}} \: = \: B_{2} \: \oplus \: B_{3}}$$
格雷码位 G3 的 K-Map
格雷码位 G3 的 K-Map 简化如下图所示 −
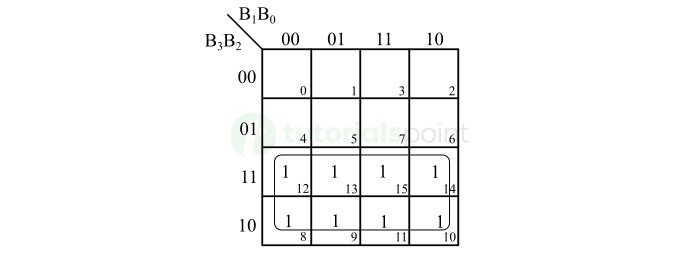
因此,格雷码位 G3 的布尔表达式为,
$$\mathrm{G_{3} \: = \: B_{3}}$$
现在让我们利用这些布尔表达式来实现二进制到格雷码转换器的逻辑电路。
下图显示了 4 位二进制码到格雷码转换器的逻辑电路图 −
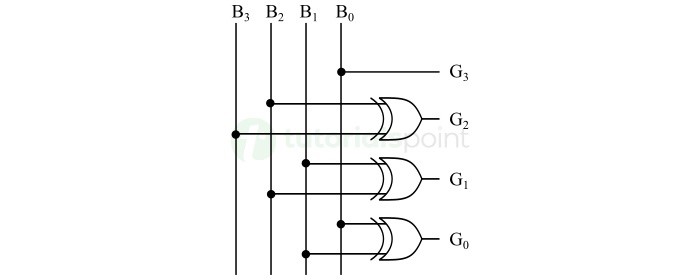
该电路可以将 4 位二进制数转换为等效的格雷码。
我们可以按照相同的程序为任意数量的位数设计二进制到格雷码转换器。


