使用二极管电阻逻辑的或门
逻辑门是一种数字电子电路,用于实现不同类型的逻辑和比较运算。我们有几种类型的逻辑门,例如或门、与门、非门、与非门、或非门等。在这里,我们将讨论使用二极管电阻逻辑实现或逻辑门,即 DL 或门。但在深入探讨 DL 或门的实现之前,让我们先讨论一下或门的基础知识。
什么是或门?
或门 是一种逻辑电路,可能具有两个或多个二进制输入,并根据输入的组合给出输出。
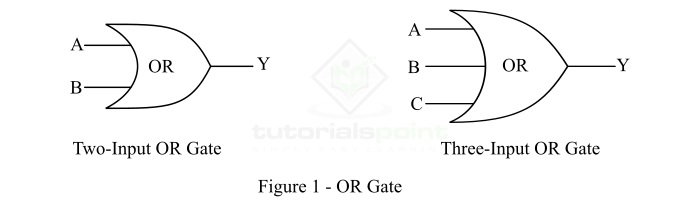
或门产生逻辑 1(高)输出,即使其输入之一处于逻辑 1(高)状态。只有当其每个输入都处于逻辑 0(低)状态时,或门才会给出逻辑 0(低)输出。因此,或门也称为任意或所有门。它也可以称为包含或门,因为它包括两个输入都可以存在的状态。图 1 显示了双输入和三输入或门的符号。
或运算
或运算用 + 表示。或门输出的布尔表达式如下所示,
$$\mathrm{Y = A+B+C+ \cdot \cdot \cdot }$$
其中,Y 是或门的输出,A、B、C… 是或门的输入变量。
逻辑门的操作可以用表示输入和输出之间逻辑关系的真值表来解释。
或门的真值表
下表是三输入或门的真值表。
| 输入 | 输出 | ||
|---|---|---|---|
| A | B | C | Y = A + B + C |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
使用二极管电阻逻辑的或门
我们可以使用二极管和电阻来实现分立的或门(称为二极管电阻逻辑)。使用二极管电阻逻辑的或门的电路图如下图 2 所示。

这里,门的输入 A 和 B 可以是 0 V 或 +5 V。使用二极管电阻逻辑的或门的操作说明如下 -
- 当 A = 0 V 且 B = 0 V 时,二极管 D1 和 D2 均关闭。因此,没有电流流过电阻器 R,所以电阻器 R 上没有电压降。因此,输出电压 Y = 0 V。
- 当 A = +5 V 且 B = 0 V 时,二极管 D1 导通,二极管 D2 截止。因此,输出电压 Y = 5 V。
- 当 A = 0 V 且 B = +5 V 时,二极管 D1 截止,二极管 D2 导通。因此,输出电压 Y = 5 V。
- 当 A = +5 V 且 B = +5 V 时,二极管 D1 和 D2 均导通。因此,输出电压 Y = 5 V。
注意 −实际上,二极管本身会产生一个小的电压降(约 0.7 V)。因此,输出电压 Y = 5 – 0.7 = 4.3 V。此输出电压被视为逻辑 1。
结论
从以上讨论中,我们可以得出结论,或门是一种用于实现二进制和运算的基本逻辑门。即使或门的任何输入处于逻辑 1 状态,它也会输出逻辑 1。只有当所有输入都处于逻辑 0 状态时,它才会输出逻辑 0。


