数字电子技术 - K-Map 最小化

什么是卡诺图?

在数字电子系统的实现中，布尔表达式的简化是最重要的步骤之一，因为它可以降低硬件复杂性和生产成本。有几种工具和方法可用于简化复杂的布尔表达式。K-Map 或卡诺图就是其中一种简化方法。K-Map 由 Maurice Karnaugh 于 1953 年开发。它是一种用于简化布尔表达式的视觉或图形方法。

当布尔表达式中的变量数小于或等于四个时，K-Map 是最有效的简化工具之一。但是，对于五个、六个或更多变量，K-Map 变得相当困难。

K-Map 或卡诺图利用二维表来简化布尔函数。随着布尔函数中变量数量的增加，该表的大小会大大增加。

图 1 显示了两个变量、三个变量和四个变量的 K-Map 的一些典型示例。

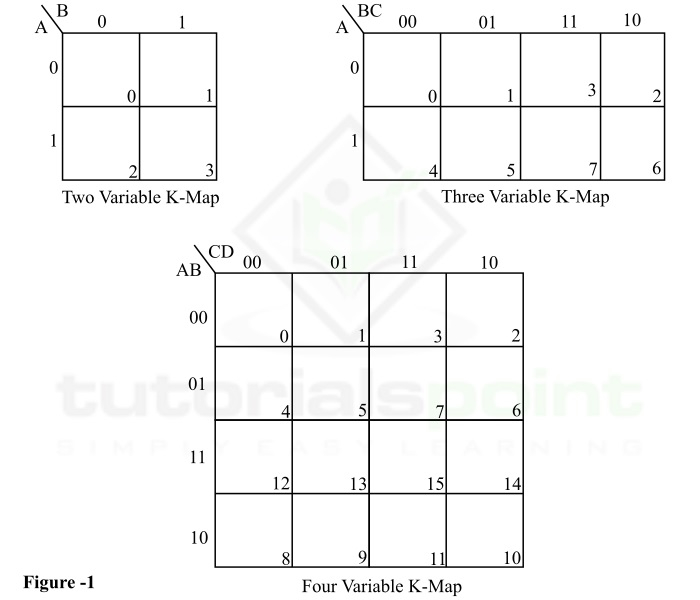
从图 1 中可以清楚地看出，卡诺图中的方块或单元的数量取决于表达式中的变量数量。

如果 n 是给定布尔函数中的变量数量，则相应的卡诺图 (K-Map) 将有 2ⁿ 个方块或单元。例如，如果布尔函数中的变量数为 3，则相应的 K-Map 将具有 8(= 2³)个单元格。

卡诺图的结构

所有卡诺图或 K-Map 都具有如图 1 所示的广义类似结构。典型的 K-Map 有一个包含某些单元格的表格。在该表的左上角，一组变量表示为 A、B、C、D。这些变量基本上是需要简化的逻辑表达式中涉及的输入变量。

这些输入变量的值以二进制形式沿其各自的边表示，即在表的顶部和左侧。

从以上示例中可以看出，K-Map 顶部和左侧的二进制数不是按其正常二进制顺序排列的，而是按格雷码排列的。格雷码用于确保两个物理相邻的单元格实际上是相邻的。这使得在最小化布尔表达式时分组过程更容易。

为了简化 K-Map 的读取，K-Map 的每个单元格都分配有一个十进制数，表示在单元格的右下角。例如，在三变量 K-Map(图 1)中，K-Map 的第二个单元格表示位模式 001，因此该单元格由其十进制等效值 1 表示。

K-Map 简化

K-Map 或卡诺图简化过程从在右侧 K-map 单元格中输入变量值开始，无论是以 SOP(乘积和)形式还是 POS(和的乘积)形式。之后，我们需要对 1 的最大数量(在 SOP 形式的情况下)或 0 的最大数量(在 POS 形式的情况下)进行分组。这些组中的每一个都必须是 2 的幂，并且必须按降序进行。

分组完成后，每个组都必须用输入变量的组合来表示，这些输入变量对应于相关行和列上的公共二进制值。最后，所有组合都表达了布尔函数的输出表达式。

卡诺图的优点

以下是卡诺图的重要优点 −

• 对于简化布尔表达式，K-map 不需要布尔代数定理的知识。
• 与其他简化技术相比，卡诺图在逻辑表达式的简化过程中涉及的步骤较少。

卡诺图的局限性

以下是卡诺图的主要局限性 −

• 卡诺图最重要的局限性是，只有当布尔表达式的变量数量较少时，它才有效。随着逻辑表达式中变量数量的增加，情况会变得相当复杂。
• 使用 K-Map 简化具有大于或等于五个变量的布尔函数非常复杂。
• 使用 K-map 很难使具有超过 5 个变量的方程式正确。

结论

卡诺图或 K-Map 是简化最多 4 个变量的布尔表达式的有效工具。它是一种简化逻辑表达式的简单方法，因为它不使用布尔代数定理。K-Map 的另一个优点是它是一种可视化的简化方法。但是，当逻辑表达式中的变量等于或大于 5 时，K-map 变得复杂且效率低下。