数字电子技术中的 6 变量 K-Map

阅读本章，了解如何使用 K-Map(卡诺图)将布尔函数简化为六个变量。让我们先简单介绍一下卡诺图(K-Map)。

卡诺图(K-Map)

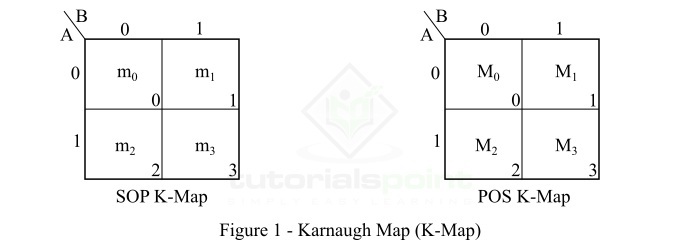
卡诺图或K-Map是一种将布尔函数简化为最小形式的图形方法。K-Map 可以定义为由相邻方块或单元格排列组成的图表或图形，其中每个单元格代表布尔表达式的特定变量组合，可以是总和形式，也可以是乘积形式。图 1 显示了典型的 2 变量 K-Map。

在实际操作中，我们通常使用最多 6 个变量的 K-map。但是，K-map 可用于任意数量的变量，但对于 5 个或更多变量，它会变得乏味。

现在，让我们讨论六变量 K-map 及其将布尔函数简化为最小形式的应用。

六变量 K-Map

六变量 K-Map 用于简化六个变量(例如 A、B、C、D、E、F)的布尔表达式。它有 64(2⁶)个相邻单元格或方块。其中，每个单元格代表函数变量的组合。

对于 SOP 形式的 6 变量布尔函数，输入变量的可能组合如下 −

$$\mathrm{\bar{A}\bar{B}\bar{C}\bar{D}\bar{E}\bar{F}, \: \bar{A}\bar{B}\bar{C}\bar{D}\bar{E}F, \: \bar{A}\bar{B}\bar{C}\bar{D}E\bar{F}, \: \dots \: ABCDEF}$$

的最小项指定这些变量的组合分别为m₀、m₁、m₂ … m₆₃。

类似地，对于POS形式的6变量布尔函数，输入变量的可能组合如下 −

$$\mathrm{\left ( A \: + \: B \: + \: C \: + \: D \: + \: E \: + \: F \right ), \: \left ( A \: + \: B \: + \: C \: + \: D \: + \: E \: + \: \bar{F} \right ), \: \left ( A \: + \: B \: + \: C \: + \: D \: + \: \bar{E} \: + \: F \right ), \: \dots \: \left ( \bar{A} \: + \: \bar{B} \: + \: \bar{C} \: + \: \bar{D} \: + \: \bar{E} \: + \: \bar{F} \right )}$$

最大项这些变量组合的名称分别为 M₀、M₁、M₂、... M₆₃。

如前所述，六变量 K 图有 64 个单元，分为 4 个块，每个块有 16 个方格。K 图上的每个单元代表一个最小项或一个最大项。在 6 变量 K 图的情况下，变量 A 和 B 的值对于每个 16 个方格块中的所有最小项(或最大项)都保持不变。

六变量 K 图的 64 个单元分为 4 个块，如下所示 −

块 1 − 这是左上角的块。此块表示从 m₀ 到 m₁₅ 的最小项(或从 M₀ 到 M₁₅ 的最大项)。在此块中，变量 A 为 0，变量 B 也为 0。

块 2 − 这是右上方的块。此块表示从 m₁₆ 到 m₃₁ 的最小项(或从 M₁₆ 到 M₃₁ 的最大项)。在此块中，变量 A 为 0，变量 B 为 1。

块 3 − 这是左下方的块。此块表示从 m₃₂ 到 m₄₇ 的最小项(或从 M₃₂ 到 M₄₇ 的最大项)。在此块中，变量 A 为 1，变量 B 为 0。

块 4 − 这是右下角的块。此块表示从 m₄₈ 到 m₆₃ 的最小项(或从 M₄₈ 到 M₆₃ 的最大项)。在此块中，变量 A 为 1，变量 B 也为 1。

简化后，6 变量 K 图可能包含 2 个方格、4 个方格、8 个方格、16 个方格、32 个方格或 64 个方格，只要涉及地图的所有四个区块即可。

在六变量 K 图上，当一个区块叠加在另一个区块之上时，该区块位于第一个区块的上方、下方或旁边，并且方格彼此重合。那么，这两个区块中的方格被认为是相邻的。还要注意，对角线元素(例如 m₁₀ 和 m₅₈、m₁₅ 和 m₆₃、m₁₈ 和 m₃₄、m₂₉ 和 m₄₅)彼此不相邻。

图 2 表示六变量 SOP K 图。

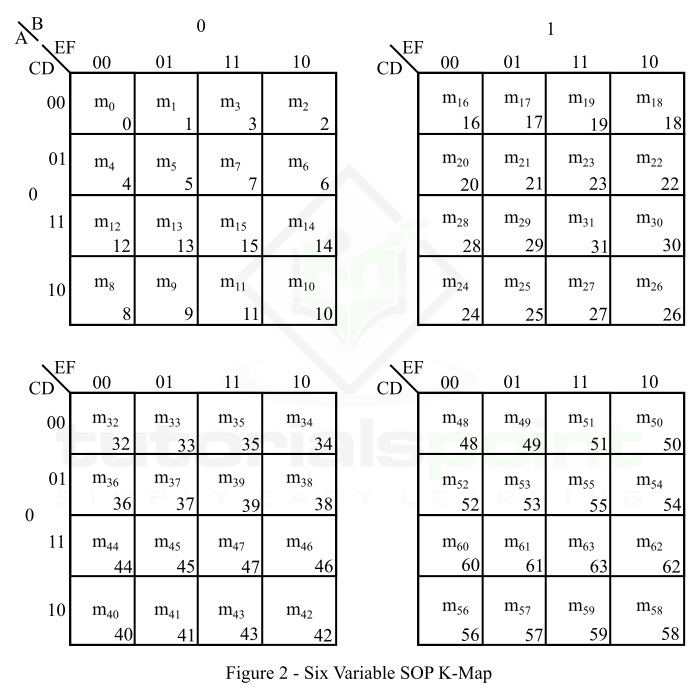
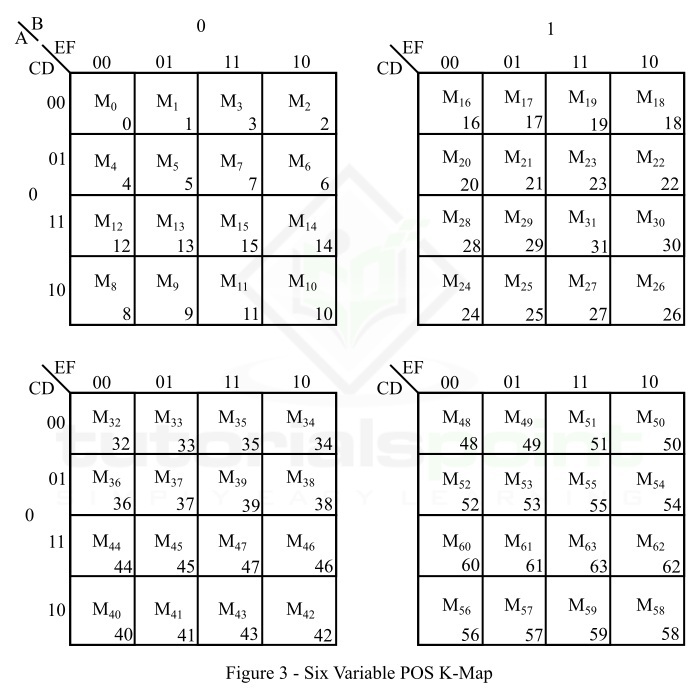
图 3 表示六变量 POS K 图。

现在，让我们借助已解决的数值示例，了解六变量 K 图在六变量布尔函数最小化中的应用。

示例 1

使用 K 图最小化以下 6 变量布尔函数。

$$\mathrm{f \: = \: \sum \: m(1, 3, 4, 5, 6, 9, 11, 12, 14, 15, 17, 19, 20, 21, 22, 23,25, 27, 28, 30, 33, 35, 36, 38, 41, 43, 44, 46, 49, 51, 52, 54, 57, 59, 60, 62)}$$

解决方案

给定布尔函数的 6 变量 SOP K-map 表示如图 4 所示。

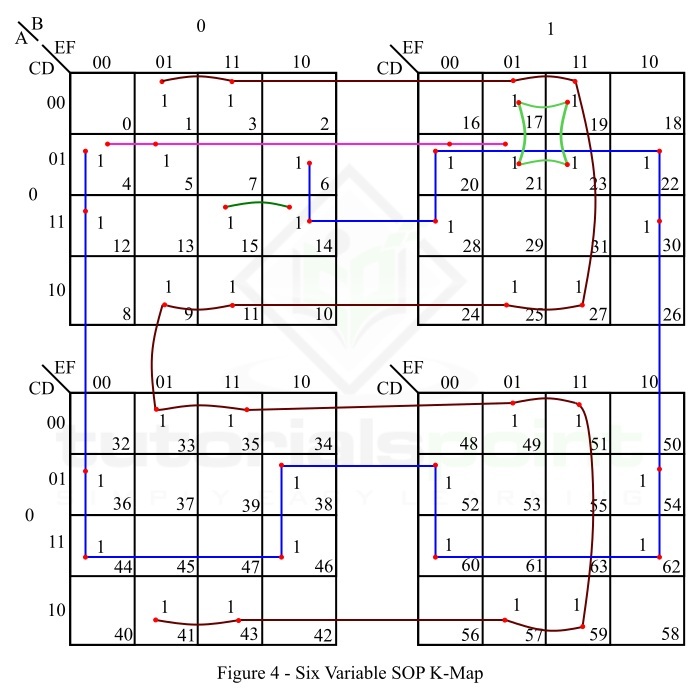
此函数的约简按以下步骤完成 −

K-map 中没有孤立的 1。

最小项 m₁ 形成一个 16 正方形，其中最小项为 m₃、m₉、m₁₁、m₁₇、m₁₉、m₂₅、m₂₇， m₃₃、m₃₅、m₄₁、m₄₃、m₄₉、m₅₁、m₅₇ 和 m₅₉。将其制作并读作 −

$$\mathrm{\bar{D}F}$$

最小项 m₄ 与最小项 m₆、m₁₂、m₁₄、m₂₀、m₂₂、m₂₈、m₃₀、m₃₆、m₃₈、m₄₄、m₄₆、m₅₂、m₅₄、m₆₀ 和 m₆₂ 形成一个 16 平方。将其制作并读作 −

$$\mathrm{\bar{F}D}$$

最小项 m₅ 可以与最小项 m₄、m₂₀ 和 m₂₁ 形成一个 4 平方数，或者与 m₁、m₁₇ 和 m₂₁ 形成一个 4 平方数。我们将用最小项 m₄、m₂₀ 和 m₂₁ 来构成它，并将其读作 −

$$\mathrm{\bar{A}\bar{C}D\bar{E}}$$

最小项 m₂₁ 与最小项 m₁₇、m₁₉ 和 m₂₃ 形成一个 4 平方数。将其制作并读作 −

$$\mathrm{\bar{A}B\bar{C}F}$$

最小项 m₁₅ 可以与最小项 m₁₁ 或 m₁₄ 组成一个 2 的平方数。我们将用 m₁₄ 来制作它，并将其读作 −

$$\mathrm{\bar{A}\bar{B}CDE}$$

将所有乘积项写成 SOP 形式。

因此，最小 SOP 表达式为，

$$\mathrm{f \left ( A,B,C,D,E,F \right ) \: = \: \bar{D}F \: + \: D\bar{F} \: + \: \bar{A}\bar{C}D\bar{E} \: + \: \bar{A}B\bar{C}F \: + \: \bar{A}\bar{B}CDE}$$

示例 2

使用 K-map 最小化以下六变量布尔函数。

$$\mathrm{f \: = \: \Pi \: M(0, 2, 7, 8, 10, 13, 16, 18, 24, 26, 29, 31,32, 34, 37, 39, 40, 42, 45, 47, 48, 50, 53, 55, 56, 58, 61, 63)}$$

解决方案

图 5 显示了给定布尔函数的 6 变量 POS K 图表示。

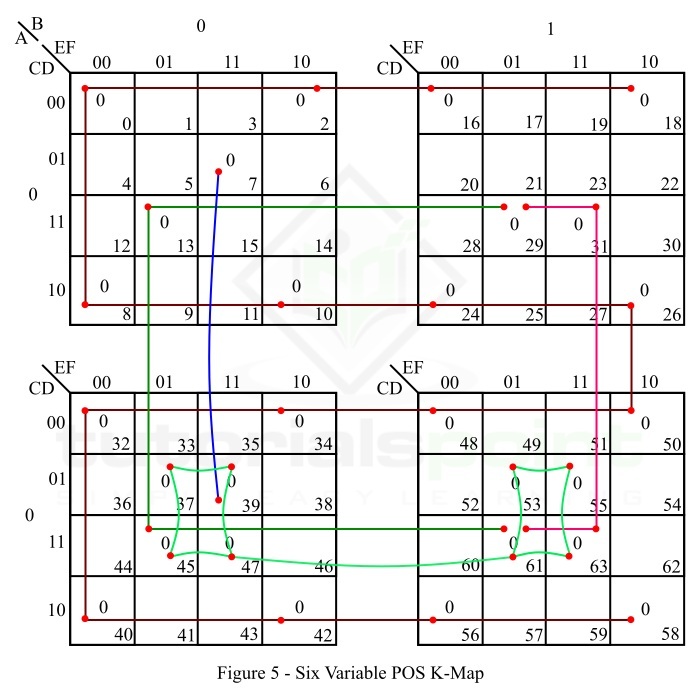
此函数的约简按以下步骤进行 −

K 图中没有孤立的 0。

最大项 M₀ 形成一个 16 方格，其中最大项为 M₂、M₈、M₁₀、M₁₆、M₁₈、M₂₄、M₂₆、M₃₂， M₃₄、M₄₀、M₄₂、M₄₈、M₅₀、M₅₆、M₅₈。将其制作并读作 −

$$\mathrm{\left ( D \: + \: F \right )}$$

最大项 M₃₇ 与最大项 M₃₉、M₄₅、M₄₇、M₅₃、M₅₅、M₆₁ 和 M₆₃ 形成一个 8 格。将其制作并读作 −

$$\mathrm{\left (\bar{A} \: + \: \bar{D} \: + \: \bar{F} \right )}$$

最大项 M₁₃ 与最大项 M₂₉、M₄₅ 和 M₆₁ 组成一个 4 格。将其制作并读作 −

$$\mathrm{\left(\bar{C} \: + \: \bar{D} \: + \: E \: + \: \bar{F} \right )}$$

最大项 M₃₁ 与 M₂₉、M₆₁ 和 M₆₃ 组成一个四方格。将其制作并读作 −

$$\mathrm{\left( \bar{B} \: + \: \bar{C} \: + \: \bar{D} \: + \: \bar{F} \right )}$$

最大项 M₇ 与最大项 M₃₉ 形成一个 2 平方数。将其写成 −

$$\mathrm{\left( B \: + \: C \: + \: E \: + \: \bar{D} \: + \: \bar{E} \: + \: \bar{F} \right )}$$

将所有求和项写成 POS 形式。

因此，给定布尔函数的最小 POS 表达式为，

$$\mathrm{f \left ( A,B,C,D,E,F \right ) \: = \: \left ( D \: + \: F \right )\left ( \bar{A} \: + \: \bar{D} \: + \: \bar{F} \right )\left( \bar{C} \: + \: \bar{D} \: + \: E \: + \: \bar{F} \right )\left( \bar{B} \: + \: \bar{C} \: + \: \bar{D} \: + \: \bar{F} \right )\left( B \: + \: C \: + \: E \: + \: \bar{D} \: + \: \bar{E} \: + \: \bar{F} \right )}$$

这都是关于六变量 K-map 及其在布尔函数最小化中的应用。尝试解决以下教程问题，以在六变量 K-map 的概念及其在减少布尔表达式中的应用方面取得优异成绩。

K-Map 上的数值问题

Q. 1 −使用 K-map 以 SOP 形式最小化以下六个变量布尔函数。

$$\mathrm{f \left ( A,B,C,D,E,F \right ) \: = \: \sum m(1, 3, 5, 7, 9, 10, 11, 12, 14, 16, 17, 19, 20, 22, 24, 25, 26, 31, 32,34, 36, 37, 39, 40, 42, 45, 49, 50, 53, 54, 57, 60, 61, 63)} $$

Q. 2 −使用 K-map 最小化以下 POS 形式的六变量布尔函数。

$$\mathrm{f \left ( A,B,C,D,E,F \right ) \: = \: \Pi M(0, 1, 3, 4, 5, 6, 8, 9, 10, 12, 14, 15, 17, 20, 21, 22, 25, 26, 27,29, 30, 32, 33, 35, 36, 37, 39, 40, 41, 42, 45, 47, 48, 50, 52, 53, 55, 56, 58, 59, 60, 62 )}$$