4 数字电子技术中的变量 K 图

已经开发出几种技术来将复杂的布尔表达式简化为最简单的形式。K 图 或 卡诺图 就是这种最小化或简化技术之一。

K 图或卡诺图是由相邻单元格排列组成的图形或图表。其中，K 图的每个单元格代表以和或乘积形式表示的特定变量组合。K 图可用于简化涉及任意数量变量的布尔函数。但是，对于涉及五个或更多变量的问题，使用 K 图简化布尔函数会变得繁琐。因此，在实际操作中，K 图仅限于六个变量。

K 图中单元格的数量取决于给定布尔函数中的变量数量。 K-map 将有 2ⁿ 个单元格或方块，其中 n 是布尔表达式中的变量数。因此，对于双变量函数，K-map 将有 2² = 4 个单元格，对于三变量布尔函数，K-map 将有 2³ = 8 个单元格，对于四变量布尔函数，K-map 将有 2⁴ = 16 个单元格，依此类推。

在这里，我们将讨论四变量 K-Map，并使用它来简化 4 个变量中的布尔函数。

四变量 K-Map

四变量 K-map 用于简化 4 个变量中的复杂布尔表达式。我们知道，一个四变量布尔表达式可以有 2⁴ = 16 种可能的变量组合。

例如，在 SOP(乘积和)形式中，

$$\mathrm{f(A,B,C,D) \: = \: \bar{A}\bar{B}\bar{C}\bar{D} \: + \: \bar{A}\bar{B}\bar{C}D \: + \: \bar{A}\bar{B}C\bar{D} \: + \: \dots \: + \: ABCD}$$

该表达式的最小项表示如下如下，

$$\mathrm{f(A,B,C,D) \: = \: m_{0} \: + \: m_{1} \: + \: m_{2} \: + \: \dotso \: + \: m_{15}}$$

在 POS(和的乘积)形式中，

$$\mathrm{f(A,B,C,D) \: = \: (A \: + \: B \: + \: C \: + \: D)(A \: + \: B \: + \: C \: + \: \overline{D} )(A \: + \: B \: + \: \overline{C} \: + \: D) \: \dotso \: (\overline{A} \: + \: \overline{B} \: + \: \overline{C} \: + \: \overline{D})}$$

该表达式的最大项表示如下，

$$\mathrm{f(A,B,C,D) \: = \: M_{0}\cdot M_{1}\cdot M_{2} \: \dotso \: M_{15}}$$

4 变量 K 图有 16 个单元，每个单元代表函数的最小项或最大项。图 1 显示了四变量布尔表达式的 SOP(乘积和)形式和 POS(和的乘积)形式。

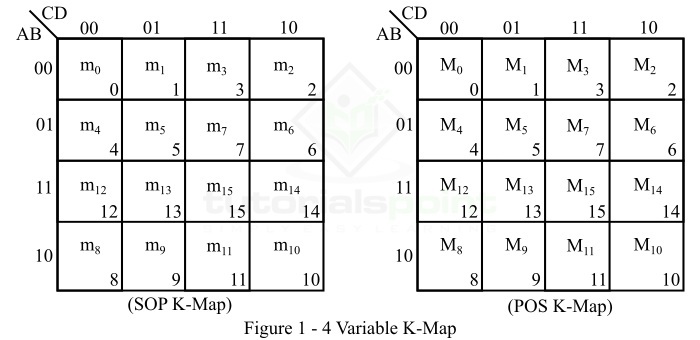
此处，列和行的二进制数字标识采用格雷码。这称为相邻排序。在这些 K 图中，图左侧的二进制数字表示任意行上变量 A 和 B 的条件，K 图顶部的二进制数字表示任意列上变量 C 和 D 的条件。单元格右下角的小数表示最小项或最大项的名称。

现在，让我们考虑一个例子来说明如何使用 4 变量 K 图简化布尔函数。

示例 1

使用 4 变量 K 图简化以下布尔表达式。

$$\mathrm{f \lgroup A,B,C,D \rgroup \: = \: \sum m \lgroup 2,3,6,7,8,10,13,15 \rgroup}$$

解决方案

给定布尔函数的 SOP K 图表示如图 2 所示。

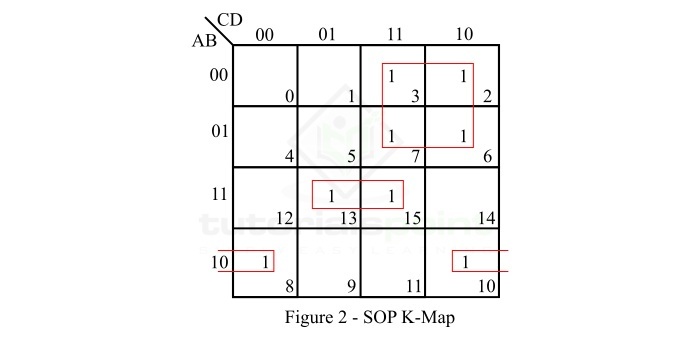
解释

函数的简化按照以下步骤进行 −

K-Map 中没有孤立的 1。

最小项 m2 可以与 m3、m6 和 m7 形成一个 4 方格。将其制作并读作 −

$$\mathrm{\bar{A}C}()$$

最小项 m8 可以与 m10 形成一个 2 方格。将其制作并读作 −

$$\mathrm{AB\bar{D}}()$$

最小项 m13 可以与 m15 形成一个 2 方格。将其制作并读作 −

$$\mathrm{(A\bar{B}D)}$$

将所有乘积写成 SOP 形式。

因此简化的 SOP 表达式为，

$$\mathrm{f(A,B,C,D) \: = \: \bar{A}C \: + \: A\bar{B}D \: + \: AB\bar{D}}$$

示例 2

使用 4 变量 K 图最小化以下布尔表达式。

$$\mathrm{f(A,B,C,D) \: = \: \prod \: M(4,6,11,14,15)}$$

解决方案

给定布尔函数的 POS K-map 表示如图 3 所示。

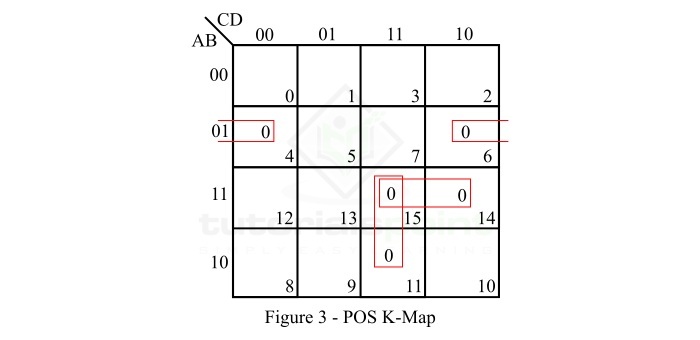
解释

给定函数的最小化按照以下步骤完成 −

K-map 中没有孤立零点。

最大项 M4 可以与 M6 形成 2-squate。将其改为 −

$$\mathrm{(A \: + \: \bar{B} \: + \: D)}$$

最大项 M11 可以与 M15 组成 2 方格。将其改为 −

$$\mathrm{(\bar{A} \: + \: \bar{C} \: + \: \bar{D})}$$

现在只剩下最大项 M₁₄。M₁₄ 可以与 M₆ 或 M₁₅ 组成 2 方格。如果我们用 M15 来做，那么读作 −

$$\mathrm{(\bar{A} \: + \: \bar{B} \: + \: \bar{C})}$$

最后，将所有求和项写成 POS 形式。

因此，给定布尔函数的简化 POS 表达式为，

$$\mathrm{f(A,B,C,D) \: = \: (A \: + \: \bar{B} \: + \: D)(\bar{A} \: + \: \bar{C} \: + \: \bar{D})(\bar{A} \: + \: \bar{B} \: + \: \bar{C})}$$

K-Map 上的数值问题

Q1. 使用 4 变量 K-map 简化以下布尔函数

$$\mathrm{f \lgroup A,B,C,D \rgroup \: = \: \sum m \lgroup 0,1,2,5,8,10,11,13,14,15 \rgroup }$$

Q2. 使用 4 变量最小化以下布尔表达式K-Map。

$$\mathrm{f \lgroup A,B,C,D \rgroup \: = \: \prod \: M \lgroup 0,2,8,10,11,13,15 \rgroup}$$

结论

这就是关于 4 变量 K-map 及其将布尔表达式最小化为最小形式的应用。从以上讨论中，我们可以得出结论，4 变量 K-map 是涉及 4 个变量的布尔表达式的图形表示，并以标准 SOP 或 POS 形式表示。这用于将标准 SOP 或 POS 形式，或 4 变量布尔表达式的最小项形式或最大项形式转换为其最小 SOP 或 POS 形式。