数字电子 - 解复用器
什么是解复用器?
解复用器是一种组合逻辑电路,它接受单个输入并将其分配到多条输出线上。解复用器也简称为DEMUX。由于解复用器用于将相同数据传输到不同的目的地,因此它也被称为数据分配器。
还有另一种组合逻辑电路,称为多路复用器,它执行与解复用器相反的操作,即接受多个输入并一次将其中一个传输到输出线。
根据定义,我们可以说解复用器是 1 对 2n 设备。图 1 显示了典型 1×2n 解复用器的功能框图。
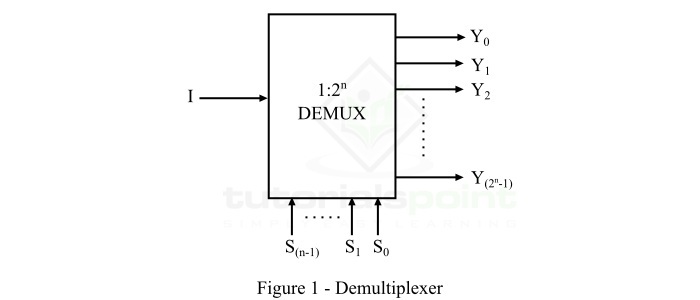
可以看出,解复用器只有一条数据输入线、2n 条输出线和 n 条选择线。应用于解复用器选择线的逻辑电平决定了输入数据将被传输到的输出通道。
解复用器电路是广泛用于数字解码器和布尔函数发生器电路的组合逻辑电路。
解复用器的类型
根据输出线的数量(2n),解复用器可分为几种类型。一些常用的解复用器类型是 −
- 1×2 解复用器
- 1×4 解复用器
现在,让我们简要讨论一下每种类型的解复用器。
1×2 解复用器
1×2 解复用器的功能框图如图 2 所示。
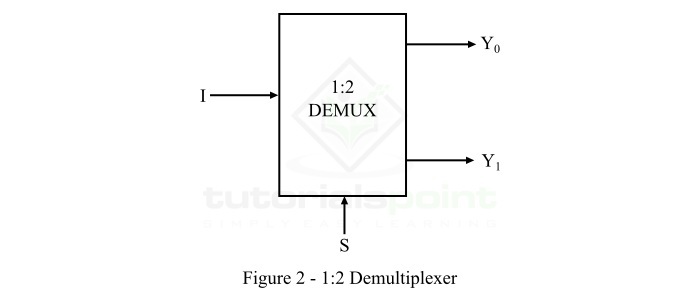
1×2 解复用器由 1 条输入线 (I)、1 条选择线 (S) 和 2 条输出线 (Y0 和 Y1) 组成。选择线上应用的逻辑电平决定了输入数据将被传输到的输出线。
可以借助下面给出的功能表来分析 1×2 解复用器的操作。
| 选择线 | 输出 | |
|---|---|---|
| S | Y1 | Y0 |
| 0 | 0 | I |
| 1 | I | 0 |
从 1×2 解复用器的这个函数表中,我们可以直接得出每个输出的布尔表达式,如下所示。
$$\mathrm{Y_{0} \: = \: \bar{S} \: I}$$
并且,
$$\mathrm{Y_{1} \: = \: S \: I}$$
1×4 解复用器
1×4 解复用器的功能框图如图 3 所示。
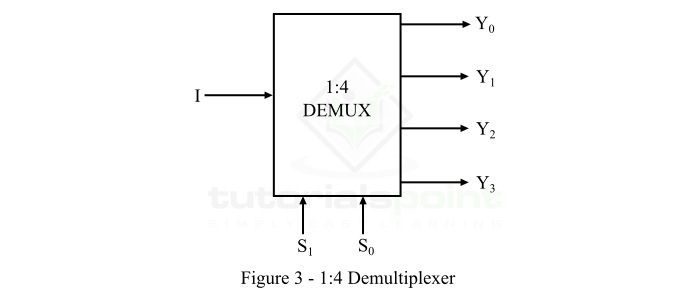
1×4解复用器有 1 条输入线 (I)、2 条选择线 (S0 和 S1) 和 4 条输出线 (Y0、Y1、Y2 和 Y3)。应用于选择线的逻辑电平决定了输入数据 (I) 将传输到的输出线。
借助下面给出的功能表,可以理解 1×4 解复用器的操作。
| 选择线 | 输出 | ||||
|---|---|---|---|---|---|
| S1 | S0 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | I |
| 0 | 1 | 0 | 0 | I | 0 |
| 1 | 0 | 0 | I | 0 | 0 |
| 1 | 1 | I | 0 | 0 | 0 |
从这个 1×4 解复用器的真值表中,我们可以直接为每个输出写出布尔表达式,如下所示。
$$\mathrm{Y_{0} \: = \: \bar{S_{1}} \: \bar{S_{0}} \: I}$$
$$\mathrm{Y_{1} \: = \: \bar{S_{1}} \: S_{0} \: I}$$
$$\mathrm{Y_{2} \: = \: S_{1} \: \bar{S_{0}} \: I}$$
$$\mathrm{Y_{3} \: = \: S_{1} \: S_{0} \: I}$$
我们可以很容易地理解上述电路的工作原理。类似地,您可以按照相同的步骤实现 1×8 解复用器和 1×16 解复用器。
高阶解复用器的实现
现在,让我们使用低阶解复用器实现以下两个高阶解复用器。
- 1×8 解复用器
- 1×16 解复用器
1×8 解复用器
在本节中,让我们使用 1×4 解复用器和 1×2 解复用器实现 1×8 解复用器。我们知道 1×4 解复用器具有单个输入、两个选择线和四个输出。而 1×8 解复用器具有单个输入、三条选择线和八个输出。
因此,我们需要在第二阶段使用两个 1×4 解复用器 才能获得最终的八个输出。由于第二阶段的输入数量为两个,因此我们需要在第一阶段使用 1×2 解复用器,以便第一阶段的输出将成为第二阶段的输入。此 1×2 解复用器的输入将是 1×8 解复用器的总输入。
假设 1×8 解复用器具有一个输入 I、三条选择线 s2、s1 和 s0 以及输出 Y7 至 Y0。 1×8 解复用器的真值表如下所示。
| 选择输入 | 输出 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| s2 | s1 | s0 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | I |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | I | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | I | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | I | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
通过考虑上述真值表,我们可以轻松地使用低阶多路复用器实现 1×8 解复用器。下图显示了 1×8 解复用器的框图。
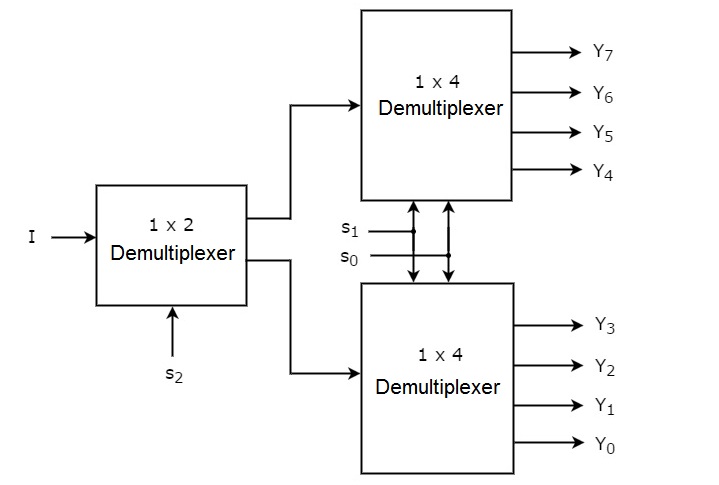
公共选择线 s1 和 s0 应用于两个 1×4 解复用器。上部 1×4 解复用器的输出为 Y7 至 Y4,下部 1×4 解复用器的输出为 Y3 至 Y0。
另一条 选择线 s2 应用于 1×2 解复用器。如果 s2 为零,则下部 1×4 解复用器的四个输出之一将等于输入 I,具体取决于选择线 s1 和 s0 的值。同样,如果 s2 为一,则上部 1×4 解复用器的四个输出之一将等于输入 I,具体取决于选择线 s1 和 s0 的值。 s0。
1×16 解复用器
在本节中,让我们使用 1×8 解复用器和 1×2 解复用器实现 1×16 解复用器。我们知道 1×8 解复用器具有单个输入、三条选择线和八个输出。而 1×16 解复用器具有单个输入、四条选择线和十六个输出。
因此,我们需要在第二阶段使用两个 1×8 解复用器 才能获得最终的十六个输出。由于第二阶段的输入数量为两个,因此我们需要在第一阶段使用 1×2 解复用器,以便第一阶段的输出将成为第二阶段的输入。此 1×2 解复用器的输入将是 1×16 解复用器的总输入。
假设 1×16 解复用器有一个输入 I、四条选择线 s3、s2、s1 和 s0 以及输出 Y15 至 Y0。下图显示了使用低阶复用器的 1×16 解复用器的框图。
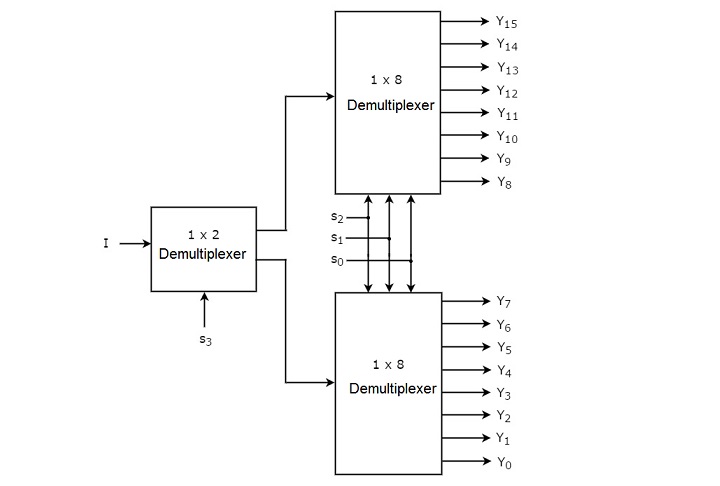
公共选择线 s2、s1 和s0 应用于两个 1×8 解复用器。上部 1×8 解复用器的输出为 Y15 至 Y8,下部 1×8 解复用器的输出为 Y7 至 Y0。
另一条 选择线 s3 应用于 1×2 解复用器。如果 s3 为零,则根据选择线 s2、s1 和 s0 的值,下部 1×8 解复用器的八个输出之一将等于输入 I。类似地,如果 s3 为 1,则根据选择线 s2、s1 和 s0 的值,上部 1×8 解复用器的 8 个输出之一将等于输入 I。
用作解复用器的集成电路 (IC)
解复用器也可以以 IC 的形式构建。有几种类型的 IC 可用作解复用器。下面列出了一些常见的 −
- 74139 IC 用作 1×4 解复用器
- 74237 IC 用作 1×8 解复用器
- 74154 IC 用作 1×16 解复用器
解复用器的优点
解复用器的重要优点如下 −
- 通过使用解复用器,我们可以提高通信系统的效率。
- 解复用器可以从混合信号流中分离出不同的信号。
- 解复用器可以解码多路复用器产生的信号。
解复用器的缺点
解复用器的主要缺点如下 −
- 使用解复用器会导致带宽浪费。
- 信号的同步会导致系统延迟。
解复用器的应用
解复用器是一种重要的组合逻辑电路,用于许多应用中。解复用器的一些重要用途如下 −
- 解复用器用于多个输入和输出设备的数据路由。
- 解复用器用于数字控制系统,从相互的信号流中选择一个信号。
- 解复用器也用于同步系统中的数据传输。
- 解复用器也用于数据采集系统。
- 解复用器可用于生成布尔函数。
- 解复用器可用于串并转换器。
- 解复用器用于 ATM 数据包的广播。
- 解复用器还可用于设计自动测试设备等。
以上就是关于解复用器、其类型和应用的全部内容。


