数字电子技术中的半加器
加法是计算机、计算器等不同电子设备执行的最基本操作之一。执行两个或多个数字(更具体地说是二进制数字)相加的电子电路称为加法器。由于逻辑电路使用二进制数字系统执行操作,因此加法器被称为二进制加法器
根据电路可以添加的位数,加法器(或二进制加法器)有两种类型 −
- 半加器
- 全加器
在本文中,我们将讨论半加器、其定义、电路图、真值表、kmap、特征方程和应用。
什么是半加器?
用于将两个二进制数字相加的组合逻辑电路称为半加器。半加器提供输出以及进位值(如果有)。半加器电路是通过连接一个异或门和一个与门来设计的。它有两个输入端和两个输出端,用于求和和进位。半加器的框图和电路图如图 1 所示。
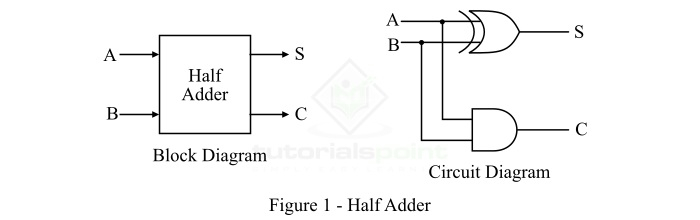
从半加器的逻辑电路图中可以看出,A 和 B 是两个输入位,S 是输出和,C 是输出进位位。
对于半加器,异或门的输出是两位之和,与门的输出是进位。虽然一次加法得到的进位不会在下一次加法中转发,因此它被称为半加器。
半加器的操作
半加器根据二进制加法规则将两个二进制数字相加。这些规则如下 −
$$\mathrm{0 \: + \: 0 \: = \: 0}$$
$$\mathrm{0 \: + \: 1 \: = \: 1}$$
$$\mathrm{1 \: + \: 0 \: = \: 1}$$
$$\mathrm{1 \: + \: 1 \: = \: 10 \: (Sum \: = \: 0 \: \& \: Carry \: = \: 1)}$$
根据这些二进制加法规则,我们可以看到前三个运算产生的和的长度为一位,而在最后一个运算(1 和 1)的情况下,和由两位组成。这里,此结果的 MSB(最高有效位)称为进位(为 1),LSB(最低有效位)称为和(为 0)。
半加器的真值表
真值表给出了逻辑电路的输入和输出之间的关系,并解释了电路的操作。以下是半加器的真值表 −
| 输入 | 输出 | ||
|---|---|---|---|
| A | B | S (Sum) | C (Carry) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
半加器的K图
我们可以使用K图(卡诺图)这种简化布尔代数的方法来确定半加器电路的和位(S)和输出进位位(C)的方程。
半加器电路的k图如图2所示。
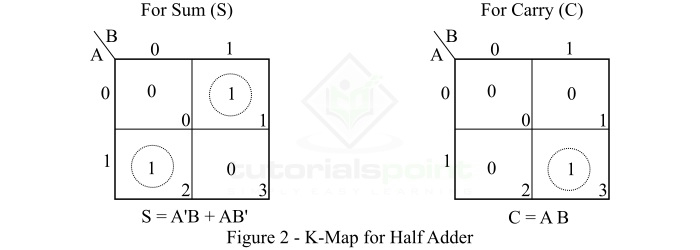
半加器的特征方程
根据二进制加法规则,可以得到半加器的特征方程,即和(S)和进位(C)的方程。这些方程如下所示 −
半加器的和 (S) 是 A 和 B 的异或。因此,
$$\mathrm{Sum, \: S \: = \: A \: \oplus B \: = \: AB' \: + \: A'B }$$
半加器的进位 (C) 是 A 和 B 的与。因此,
$$\mathrm{Carry, \: C \: = \: A \cdot B }$$
半加器的应用
以下是半加器 −
的一些重要应用- 半加器用于计算机处理器的 ALU(算术逻辑单元)中,用于添加二进制位。
- 半加器用于实现全加器电路。
- 半加器用于计算器。
- 半加器用于计算地址和表。
结论
从以上讨论中,我们可以得出结论,半加器是不同电子设备中用于执行两个二进制数字相加的基本算术电路之一。半加器的主要缺点是它不能添加从上一级相加中获得的进位。为了克服这个缺点,电子系统中使用了全加器。


