数模转换器

数模转换器 (DAC) 将数字输入信号转换为模拟输出信号。数字信号用二进制代码表示，它是位 0 和 1 的组合，而模拟信号是连续时间函数。

本章详细介绍了数模转换器。DAC 的框图如下图所示 −

数模转换器 (DAC) 由多个二进制输入和一个输出组成。一般来说，DAC 的二进制输入数量是 2 的幂。

数模转换器的类型

根据构造和结构，有两种类型的数模转换器，它们是 −

• 加权电阻 DAC
• R-2R 梯形 DAC

以下部分将详细讨论这两种类型的 DAC。

加权电阻 DAC

加权电阻 DAC 通过在反相加法器电路中使用二进制加权电阻来产生模拟输出，该输出几乎等于数字(二进制​​)输入。简而言之，二进制加权电阻 DAC 称为加权电阻 DAC。

下图显示了 3 位二进制加权电阻 DAC 的电路图 −

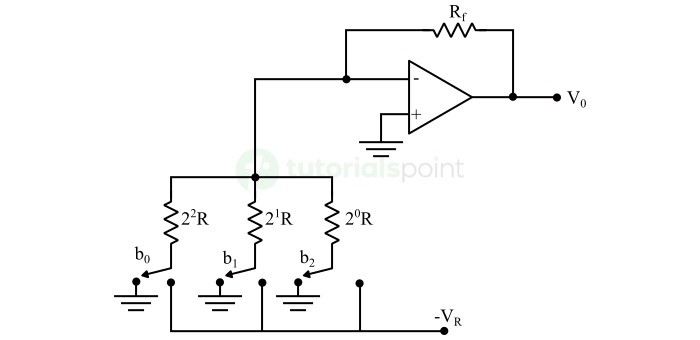
回想一下，二进制数的位只能有两个值之一。即 0 或 1。假设 3 位二进制输入为 b₂b₁b₀。这里，位 b₂ 和 b₀ 分别表示最高有效位 (MSB) 和最低有效位 (LSB)。

当相应的输入位等于"0"时，上图所示的数字开关将接地。类似地，当相应的输入位等于"1"时，上图所示的数字开关将连接到负参考电压 −V_R。

在上述电路中，运算放大器的非反相输入端接地。这意味着在运算放大器的非反相输入端施加零伏。

根据虚短概念，运算放大器反相输入端的电压与其非反相输入端的电压相同。因此，反相输入端节点的电压将为零伏。

反相输入端节点的节点方程为 −

$$\mathrm{\frac{0 \: + \: V_{R}b_{2}}{2^{0}R} \: + \: \frac{0 \: + \: V_{R}b_{1}}{2^{1}R} \: + \: \frac{0 \: + \: V_{R}b_{0}}{2^{2}R} \: + \: \frac{0 \: - \: V_{0}}{R_{f}} \: = \: 0}$$

$$\mathrm{\右箭头 \: \frac{V_{0}}{R_{f}} \: = \: \frac{V_{R}b_{2}}{2^{0}R} \: + \: \frac{V_{R}b_{1}}{2^{1}R} \: + \: \frac{V_{R}b_{0}}{2^{2}R}}$$

$$\mathrm{\右箭头 \: V_{0} \: = \: \frac{V_{R}R_{f}}{R}(\frac{b_{2}}{2^{0}} \: + \: \frac{b_{1}}{2^{1}} \: + \: \frac{b_{0}}{2^{2}})}$$

代入上式，R = 2R_f，

$$\mathrm{V_{0} \: = \: \frac{V_{R}R_{f}}{2R_{f}}(\frac{b_{2}}{2^{0}} \: + \: \frac{b_{1}}{2^{1}} \: + \: \frac{b_{0}}{2^{2}})}$$

$$\mathrm{\因此 \: V_{0} \: = \: \frac{V_{R}}{2}(\frac{b_{2}}{2^{0}} \: + \: \frac{b_{1}}{2^{1}} \: + \: \frac{b_{0}}{2^{2}})}$$

上述等式表示 3 位二进制加权电阻 DAC 的输出电压方程。由于二进制(数字)输入的位数为 3，因此，通过将二进制输入从 000 变为 111，对于固定参考电压 V_R，我们将获得 7 种可能的输出电压值。

我们可以根据 3 位二进制加权电阻 DAC 的输出电压方程，写出如下所示的 N 位二进制加权电阻 DAC 的广义输出电压方程。

$$\mathrm{\因此 \: V_{0} \: = \: \frac{V_{R}}{2}(\frac{b_{N-1}}{2^{0}} \: + \: \frac{b_{N-2}}{2^{1}} \: + \dotso \: + \: \frac{b_{0}}{2^{N-1}})}$$

加权电阻 DAC 的缺点

二进制加权电阻 DAC 的缺点如下 −

• 随着数字输入中位数的增加，LSB 和 MSB 对应的电阻值之间的差异将增大。
• 随着数字输入中位数的增加，设计更精确的电阻器会变得更加困难。

R-2R 梯形 DAC

R-2R 梯形 DAC 克服了二进制加权电阻 DAC 的缺点。顾名思义，R-2R 梯形 DAC 通过在反相加法器电路中使用 R-2R 梯形网络产生模拟输出，该输出几乎等于数字(二进制​​)输入。

3 位 R-2R 梯形 DAC 的电路图如下图所示 −

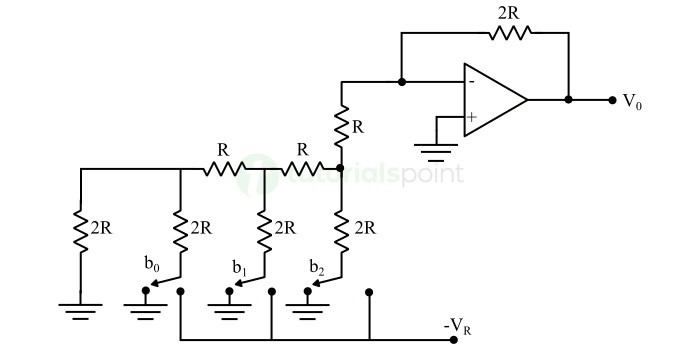
回想一下，二进制数的位只能有两个值之一。即 0 或 1。假设 3 位二进制输入为 b₂b₁b₀。这里，位 b₂ 和 b₀ 分别表示最高有效位 (MSB) 和最低有效位 (LSB)。

当相应的输入位等于"0"时，上图所示的数字开关将接地。同样，当相应的输入位等于"1"时，上图所示的数字开关将连接到负参考电压 −V_R。

很难得到 R-2R 梯形 DAC 的广义输出电压方程。但是我们可以轻松找到 R-2R 梯形 DAC 针对单个二进制输入组合的模拟输出电压值。

R-2R 梯形 DAC 的优点

R-2R 梯形 DAC 的优点如下 −

• R-2R 梯形 DAC 仅包含两个电阻值:R 和 2R。因此，选择和设计更精确的电阻器很容易。
• 如果数字输入中存在更多位数，那么我们必须另外包含所需数量的 R-2R 部分。

由于上述优势，R-2R 梯形 DAC 优于二进制加权电阻 DAC。

DAC 的重要参数

以下是我们在为特定应用选择数模转换器时必须考虑的一些关键参数和因素 −

分辨率

数模转换器可以产生的离散输出电平数称为其分辨率。为了获得更平滑和准确的模拟输出信号，数模转换器的分辨率必须非常高。DAC 的分辨率通常以位数来衡量。

让我们了解 DAC 分辨率的重要性。假设一个 DAC 可以处理 8 位，它可以表示 2⁸ = 256 个离散输出值。另一方面，如果 DAC 可以处理 16 位，那么它就能够表示 2¹⁶ = 65536 个离散输出值。因此，与 8 位 DAC 相比，16 位 DAC 可以更平滑、更准确地表示模拟格式的数字信号。

精度

数模转换器的精度是衡量输出模拟信号与输入数字信号的接近程度的标准。DAC 的高精度是产生高精度模拟输出信号的重要因素。

功耗

该因素提供有关数模转换器在运行过程中消耗的功率的信息。理想情况下，数模转换器必须节能，这样才能延长电池寿命并最大限度地降低运营成本。

运行速度

数模转换器的运行速度表示 DAC 将数字信号转换为模拟信号的速率。通常，DAC 的速度以每秒样本数 (S/s) 或兆赫 (MHz) 为单位。

数模转换器的运行速度还决定了 DAC 可以准确生成的模拟输出信号的最大频率。

在实时信号处理、快速波形生成、高速通信等应用中使用的数模转换器必须具有相当高的速度。

噪声性能

数模转换器的噪声性能表示在转换过程中可能引入到输出信号中的噪声量。不必要的噪声会影响信噪比，从而影响信号质量。因此，我们应尽可能降低噪声以获得高质量的输出模拟信号。

数模转换器的应用

数模转换器广泛应用于数字电子领域的各种应用。数模转换器的主要功能是将数字信号转换为模拟格式。

以下是一些使用数模转换器的常见设备和系统 −

• 音频放大器和播放系统
• 视频编码器系统
• 数据采集系统
• 测试和测量仪器的校准
• 电机控制电路
• 数字信号处理器
• 电信系统等

结论

数模转换器用于电子领域，提供数字输入和模拟输出之间的接口。在本章中，我们详细解释了模数转换器的类型和应用。