从 NOR 门实现 XOR 门
为了执行众多逻辑过程,逻辑门是数字电路设计中的关键元素。当输入彼此不同时,会产生高输出的逻辑门是 XOR(异或)门。使用 NOR 门创建 XOR 门是一种有趣的策略,将在本教程中讨论。了解此实现有助于我们更好地掌握逻辑门之间的灵活性和关系。
什么是 XOR 门?
数字电路中经常使用的另一个基本逻辑门是 XOR(异或)门。当有奇数个高输入时,它会生成高输出。换句话说,只有当输入彼此不同时,输出才为高电平。
异或门的真值表
双输入异或门的真值表如下 −
| 输入 A | 输入 B | 输出 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
双输入 XOR 门的布尔表达式为 −
$$\mathrm{Output \: = \: A \: \oplus \: B}$$
其中 '$\mathrm{\oplus}$' 表示 XOR 运算。
NOR 门
NOR 门是一种逻辑门,先执行逻辑或 (OR),然后执行逻辑非 (NOT)。它从两个或多个输入信号生成单个输出信号。只有当 NOR 门的所有输入都为低电平 (0) 时,输出才会为高电平 (1),对于所有其他输入配置,输出将为低电平 (0)。
NOR 门的真值表
双输入 NOR 门的真值表如下 −
| 输入 A | 输入 B | 输出 |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
双输入 NOR 门的布尔表达式为 −
$$\mathrm{Output \: = \: \thicksim \: (A \: + \: B)}$$
其中 '~' 表示逻辑非 (NOT),'+' 表示逻辑或 (OR)。
使用 NOR 门可以实现更多逻辑门和复杂的数字电路,NOR 门在数字电路中经常使用。由于它们被视为通用门,因此任何其他逻辑门或电路都只能由 NOR 门构建。
从 NOR 门实现 XOR 门
仅使用 NOR 门创建 XOR 门的电路图至少需要五个 NOR 门。五个以上的"或非"门还可以包含一个"异或"门。附图中显示了使用五个 NOR 门的 XOR 门的示意图。
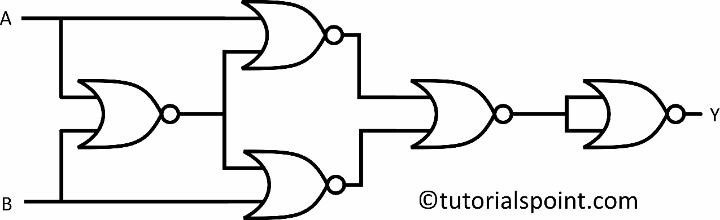
$$\mathrm{Y \: = \: (A \: \overline{B} \: + \: \overline{A} \: B)}$$
以下是如何从上述电路 − 获得 XOR 门的输出
最左边的 NOR 门有输入 A 和 B,其输出为 $\mathrm{\overline{A+B}}$
上方 NOR 门的输入为 A 和$\mathrm{\overline{A+B}}$ 输出为 $\mathrm{\overline{A \: + \: \overline{A+B}}}$
同样,下方 NOR 门的输入为 B 和 $\mathrm{\overline{A+B}}$ 输出为 $\mathrm{\overline{B \: + \: \overline{A+B}}}$
第四个 NOR 门的输入为上方和下方 NOR 门的输出,即 $\mathrm{\overline{A \: + \: \overline{A+B}}}$ 和 $\mathrm{\overline{B \: + \: \overline{A+B}}}$
第 4 个 NOR 门的输出 = $\mathrm{\overline{\overline{A \: + \: \overline{A+B}} \: + \: \overline{B \: + \: \overline{A+B}}}}$
$\mathrm{= \: \overline{\overline{A}\cdot \: \overline{(\overline{A \: + \: B})} \: + \: \overline{B}\cdot \: \overline{(\overline{A \: + \: B})}}}$
$\mathrm{\overline{\overline{A}\cdot \: (A \: + \: B) \: + \: \overline{B}\cdot \: (A \: + \: B)}}$
$\mathrm{\overline{\overline{A}\cdot \: A \: + \: \overline{A}\cdot \: B \: + \: \overline{B}\cdot \: A \: + \: \overline{B}\cdot \: B}}$
$\mathrm{\overline{\overline{A}\cdot \: B \: + \: \overline{B}\cdot \: A}}$
现在,这是最后一个或第五个 NOR 门的输入。该 NOR 门的输出是其输入的反转。因此,上述电路的最终输出为,$\mathrm{\overline{\overline{B\cdot \overline{A} \: + \: \overline{B}\cdot \: A}}}$ 或,$\mathrm{Y \: = \: (A\cdot \overline{B} \: + \: \overline{A}\cdot \: B)}$
这是 XOR 门的输出。因此,上述基于 NOR 门的电路是 XOR 门的电路。
因此,上述电路的输出与 XOR 门的输出相同。因此,上述电路表示使用 NAND 门的异或门的电路图。


