数字电子技术 - N 位并行加法器
本文首先简要介绍一下二进制加法器和二进制加法规则。在数字电子技术中,加法器或二进制加法器是一种组合数字电路,可执行两个或多个二进制数字的加法。两位二进制加法遵循以下四个规则 −
$$\mathrm{0 \: + \: 0 \: = \: 0}$$
$$\mathrm{0 \: + \: 1 \: = \: 1}$$
$$\mathrm{1 \: + \: 0 \: = \: 1}$$
$$\mathrm{1 \: + \: 1 \: = \: 10 (总和 \: = \: 0;进位 \: = \: 1)}$$
前三个操作产生的和的位长为一位二进制数。但是,最后一个组合的和,即当被加数和加数都等于 1 时,二进制和由两位二进制数组成,即和位和进位。最高有效位是进位位,而最低有效位是和位。
我们还需要全加器电路的知识,以便更好地理解 N 位并行加法器的实现和操作。下面描述了全加器及其框图和真值表。
什么是全加器?
将两个位和一个进位相加并产生一个和位和一个进位作为输出的组合数字电路称为全加器 (FA)。
换句话说,可以将三个输入位相加并产生两个输出位(即和位和进位)的二进制加法器电路称为全加器。全加器的框图如图 1 所示。
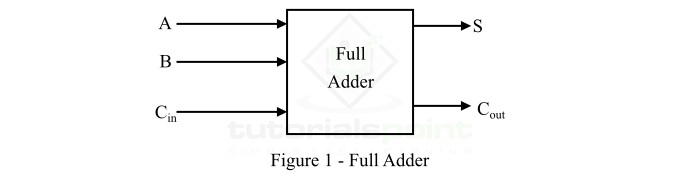
这里,A 和 B 是输入位,Cin 是来自先前总和的输入进位位,S 是输出总和位,Cout 是输出进位位。
从下面给出的真值表中可以很容易地理解全加器电路的操作。
| 输入 | 输出 | |||
|---|---|---|---|---|
| A | B | Cin | S | Cout |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
现在,让我们讨论使用全加器实现 N 位并行加法器。
N 位并行加法器
并行加法器是一种二进制加法器电路,用于将两个 N 位二进制数相加(例如,要将 4 位二进制数相加,我们使用 4 位并行加法器,依此类推)。顾名思义,并行加法器是一种数字组合电路,它以并行形式将两个二进制数相加,并以并行形式生成这些二进制数的算术和。
正如我们上面提到的,全加器只能执行由两个输入位和一个输入进位组成的两个一位二进制数的加法,即三位的加法。但在实际操作中,我们必须将长度超过一位的二进制数相加。要将这些二进制数相加,我们使用并行二进制加法器,该加法器能够将任意位长(例如 4 位、5 位等)的两个二进制数相加。
我们可以借助以链式连接的全加器来实现 N 位并行加法器。使用全加器的 N 位并行加法器的框图表示如图 2 所示。

从 N 位并行加法器的框图中可以看出,每个全加器的进位输出都连接到链中下一个更高级别全加器的进位输入端。
实现并行加法器的全加器数量取决于要相加的两个二进制数的位数。因此,N 位并行加法器需要 N 个全加器以并行形式执行加法。例如,2 位并行加法器需要 2 个全加器,4 位并行加法器由 4 个全加器组成,依此类推。
N 位并行加法器电路的工作原理
图 2 所示的 N 位并行加法器的工作原理可按以下步骤描述 −
- 最初,全加器 FA1 将两个输入位 A1 和 B1 与输入进位位 Cin 相加,并生成输出和位 S1 和进位位 C1,后者被转发到链中的下一个加法器 (FA2)。和位 S1 是输出和的最低有效位。
- 在下一阶段,全加器电路 FA2 变为活动状态,并将输入位 A2 和 B2 与 C1 相加。它生成和位 S2(输出和的第二位)和进位 C2(连接到链中的下一个全加器 FA3)。
- 此过程将持续到最后一个全加器,即链中的 FAn。全加器使用进位输入 C(n-1) 与输入位 An 和 Bn 相加,得到输出和 Sn 的最后一位以及最后一个输出进位位 Cn。
并行加法器的优点
下面列出了并行加法器的一些重要优点 −
- 并行加法器同时添加位。
- 它使二进制数的加法更快。
- 并行加法器更经济。
并行加法器的缺点
并行加法器的主要缺点是传播延迟。因为在并行加法器中,前一个加法的进位必须传播到下一个加法器,这需要一些时间。这会导致加法中出现明显的传播延迟。这种传播延迟与二进制数的位数成正比。
并行加法器的应用
并行加法器的重要应用如下 −
- 并行加法器用于重度计算应用的算术逻辑单元。
- 并行加法器还用于并行计算的并行蜂窝自动机。
- 并行加法器用于将 BCD 转换为余 1 代码。
- 并行加法器还用于乘法算法的分析。
结论
我们可以得出结论,n 位并行加法器是一种组合数字电路,它使用 n 个全加器以并行形式将两个二进制数相加。并行加法器同时执行位的加法,因此提高了二进制加法的速度。


