数字电子中的 XNOR 门
XNOR 门是一种派生逻辑门,是 XOR 门和非门的组合。因此,它产生"NOTed XOR"输出。
在本章中,我们将解释 XNOR 逻辑门的基本理论、其工作原理、电路图和应用。那么,让我们从 XNOR 门的基本定义开始。
什么是 XNOR 门?
XNOR 门是一种具有两个输入和一个输出的逻辑门。
仅当两个输入相同时,即两个输入都为高或两个输入都为低时,XNOR 门的输出才为高。如果输入不同,即一个为高而另一个为低,则输出为低或逻辑 0。
由于 XNOR 门在其两个输入相似时产生高输出,因此它也被称为相等检测器。
XNOR 门也称为异或门或异或门。
实际上,XNOR 门是两个逻辑门的组合,即 XOR 门和非门。因此,
XNOR 门 = XOR 门 + 非门
重要的是要记住,没有像 XNOR 门那样具有三个或更多输入的东西。为了获得具有两个以上输入的 XNOR 门,我们将多个双输入 XNOR 门组合在一起。
XNOR 门的逻辑符号
下图显示了双输入 XNOR 门的逻辑符号。

右端的气泡表示 NOT 操作。变量 A 和 B 表示输入线,而 Y 表示输出线。
XNOR 门的真值表
XNOR 门的真值表提供有关其操作以及输入和输出之间关系的信息。
双输入 XNOR 门的真值表如下所示 −
| 输入 | 输出 | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
从该真值表中可以看出,当 XNOR 门的两个输入相同(即 0 和 0 或 1 和 1)时,XNOR 门会产生高电平或逻辑 1 输出。否则,它会给出低电平或逻辑 0 输出。
XNOR 门的布尔表达式
布尔表达式是一个逻辑函数,它以数学方式描述 XNOR 门的输入和输出之间的关系。
双输入 XNOR 门的布尔表达式如下所示 −
$$\mathrm{Y \: = \: A \: \odot \: B}$$
这也可以表示为,
$$\mathrm{Y \: = \: AB \: + \: \bar{AB}}$$
这里,A 和 B 是输入变量,而 Y 是输出变量。
XNOR 门的工作原理
下面解释了双输入 XNOR 门在不同输入组合下的操作 −
- 如果 A = 0 且 B = 0,则 XNOR 门的输出为 Y = 1。
- 如果 A = 0 且 B = 1,则 XNOR 门的输出为 Y = 0。
- 如果 A = 1 且 B = 0,则 XNOR 门的输出为 Y = 0。
- 如果 A = 1 且 B = 1,则 XNOR 门的输出为 Y = 1。
因此,我们可以看到,对于相似的输入,输出为高电平或逻辑 1。对于不同的输入,输出为低电平或逻辑 0。
使用开关的 XNOR 门
我们可以借助两个开关、一个电池和一盏灯来实现 XNOR 门逻辑。
以下是代表 XNOR 逻辑门的电路。
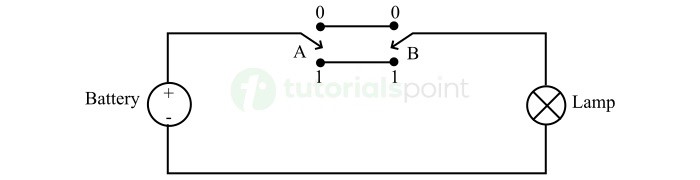
在此电路中,当两个开关 A 和 B 处于同一电平,即 0 和 0 或 1 和 1 时。电流流过灯的路径是闭合的。这样灯就会亮,并表示高电平或逻辑 1 输出。
如果开关处于不同的电平,即一个处于电平 0,另一个处于电平 1。电池和灯之间没有完整的路径。因此,灯不会发光,并表示低电平或逻辑 0 输出。
因此,上面显示的开关电路实现了 XNOR 逻辑操作。
XNOR 门作为反相器
XNOR 门可以用作反相器。如果我们将 XNOR 门的一条输入线连接到低电平或逻辑 0 信号,并将输入信号应用于另一条输入线。然后,XNOR 门的输出将是所应用输入的补码。
下图描绘了用作反相器的 XNOR 门的逻辑电路。

我们还可以借助布尔表达式来解释此操作,如下所示。
$$\mathrm{Y \: = \: AB \: + \: \bar{AB}}$$
如果 B 设置为逻辑 0,则
$$\mathrm{Y \: = \: A\cdot0 \: + \: \bar{A}\cdot1 \: = \: \bar{A}}$$
因此,如果一个输入 XNOR 门与逻辑 0 绑定,则该门将用作反相器。
XNOR 门作为缓冲器
XNOR 门也可以用作缓冲器。如果我们将 XNOR 门的一个输入连接到逻辑 1,并将输入信号应用于另一条输入线。 XNOR 门的输出将与所应用的输入相同,即 XNOR 门将用作缓冲器。
下图显示了用作缓冲器的 XNOR 门。

从逻辑上讲,我们可以通过下面的布尔表达式证明此操作。
$$\mathrm{Y \: = \: AB \: + \: \bar{AB}}$$
如果 B 设置为逻辑 1,则
$$\mathrm{Y \: = \: A\cdot1 \: + \: \bar{A}\cdot0 \: = \: A}$$
因此,一个输入设置为逻辑 1 的 XNOR 门充当缓冲器。
XNOR 门的应用
XNOR 门广泛应用于众多数字电路和系统中。XNOR 门的一些主要应用如下 −
- XNOR 门用于数字通信系统中,以检测数据传输期间发生的错误。
- XNOR 门充当相等检测器。因此,它也用于比较二进制数据或信号。
- XNOR 门还用于设计数字游戏系统和逻辑谜题。
结论
总之,XNOR 门或异或非门是用于各种数字电子应用的逻辑门。它是一个双输入逻辑门。
XNOR 门独特的相等性检测功能广泛应用于数字信号比较和数据传输错误检查。
在本章中,我们解释了 XNOR 门的基本理论和工作原理及其主要应用。


