BCD 到余 3 转换
数字电子技术中用于将二进制编码的十进制数转换为等效余 3 代码的一种代码转换器称为 BCD 到余 3 转换器。
因此,对于 BCD 到余 3 代码转换器,输入是 8421 BCD 代码,输出是 XS-3 代码。
以下是 BCD 到余 3 代码转换器的真值表 −
| BCD 代码 | 余 3 代码 | ||||||
|---|---|---|---|---|---|---|---|
| B3 | B2 | B1 | B0 | X3 | X2 | X1 | X0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | X | X | X | X |
| 1 | 0 | 1 | 1 | X | X | X | X |
| 1 | 1 | 0 | 0 | X | X | X | X |
| 1 | 1 | 0 | 1 | X | X | X | X |
| 1 | 1 | 1 | 0 | X | X | X | X |
| 1 | 1 | 1 | 1 | X | X | X | X |
让我们使用 K-map 解决真值表,以得出 XS-3 输出位 X0、X1、X2 和 X3 的布尔表达式。
XS-3 位 X0 的 K-Map>
下图显示了 XS-3 位 X0 的 K-map 简化 −
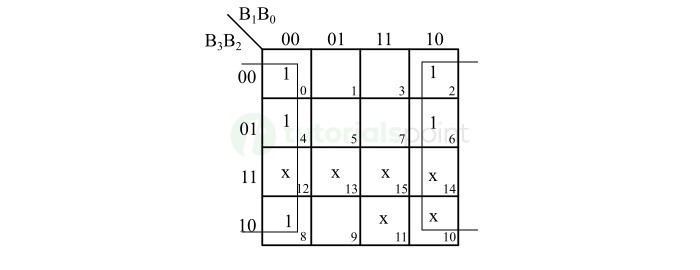
简化此 K-map 后,我们得到以下布尔表达式,
$$\mathrm{X_{0} \: = \: \overline{B_{0}}}$$
XS-3 位 X1 的 K-Map>
XS-3 位 X1 的 K-map 简化如下所示 −
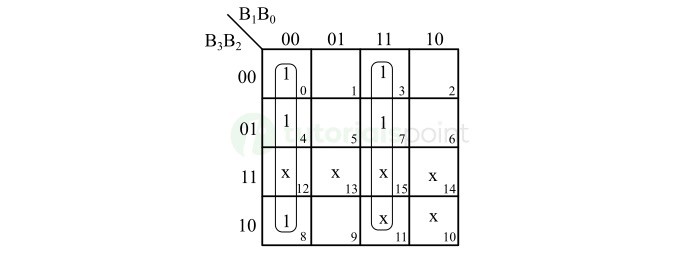
此 K-map 简化给出以下布尔表达式,
$$\mathrm{X_{1} \: = \: \overline{B_{1}} \: \overline{B_{0}} \: + \: B_{1} \: B_{0}}$$
XS-3 位 X2 的 K-Map>
下图显示了 XS-3 位 X2 的 K-map 简化。
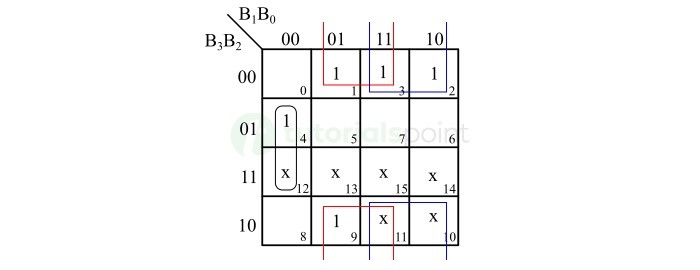
简化此 K-map 后,我们得到以下布尔表达式,
$$\mathrm{X_{2} \: = \: B_{2} \: B_{1} \: + \: \overline{B_{2}} \: B_{0} \: + \: B_{2} \: \overline{B_{1}} \: \overline{B_{0}}}$$
XS-3 位 X3 的 K-Map>
下图中描绘了 XS-3 位 X3 的 K-map 简化 −
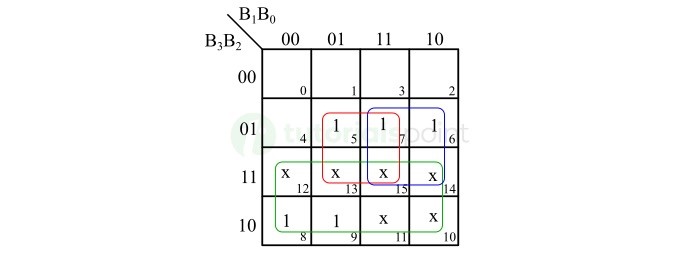
此 K-map 给出以下布尔表达式,
$$\mathrm{X_{3} \: = \: B_{3} \: + \: B_{2} \: B_{1} \: + \: B_{2} \: B_{0}}$$
BCD 到 XS-3 转换器的逻辑电路图如下图所示 −
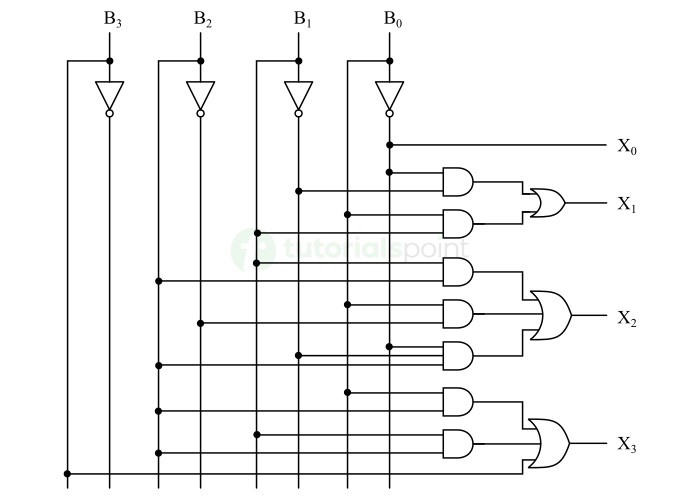
该电路将 4 位 BCD 码转换为等效的 XS-3 码。


