数字电子 - 多路复用器
接受多个数据输入并允许其中一次只允许一个数据流过输出的数字逻辑电路称为多路复用器或 MUX。本文旨在解释数字电子中的多路复用器、其框图、功能和不同类型。那么,让我们从多路复用器的基本介绍开始吧
什么是多路复用器?
如前所述,多路复用器,也称为MUX,是一种组合逻辑电路,旨在接受多个输入信号并仅通过输出线传输其中一个。简单来说,多路复用器是一种数字逻辑设备,它从 N 个(N = 2n)输入数据源中选择一个,并将所选数据传输到单个输出线。
多路复用器也称为数据选择器,因为它从多个中选择一个。典型的2n:1多路复用器的框图如图 1 所示。
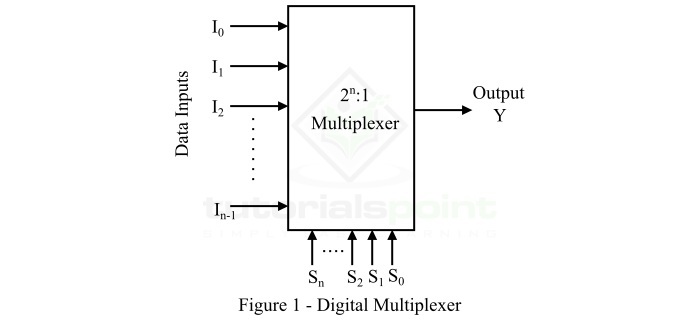
对于多路复用器,通过SELECT 线来控制流过输出线的所需数据输入的选择。在图 1 的多路复用器框图中,I0、I1、... In-1,即 (2n) 是输入线,"n" 是选择线。这些选择线将确定哪个输入要路由到输出。
因此,多路复用器用作多位置开关,其操作由数字信号控制。这些数字控制信号应用于选择线,以确定哪个数据输入将切换到输出线。
多路复用器的功能
多路复用器是一种数字逻辑设备,用于执行数据的多路复用。其中,多路复用只是意味着数据共享。从技术上讲,当从多个输入数据源中选择特定数据并将所选数据传输到单个输出通道时,这称为多路复用。
多路复用有两种类型,即频率多路复用和时间多路复用。
当系统中有多个设备连接到一条传输线时。在任何时间点,只有一个设备使用该线路传输数据,这称为时间多路复用。另一方面,当多个设备共享一条公共线路以不同的频率传输数据时,这称为频率多路复用。
多路复用器的类型
根据输入数据线和选择线,多路复用器可以有几种类型。但是,在本文中,我们将仅讨论以下三种类型的多路复用器 −
- 2×1 多路复用器
- 4×1 多路复用器
让我们分别讨论这三种多路复用器。
2×1 多路复用器
2×1 多路复用器的框图如图 2 所示。2×1 多路复用器是基本的双输入多路复用器,具有两个数据输入线,指定为 I0 和 I1,一个数据选择线,表示为 S,一个输出线,表示为 Y。2×1 多路复用器用于将两个 1 位数据源连接到一个公共指定。
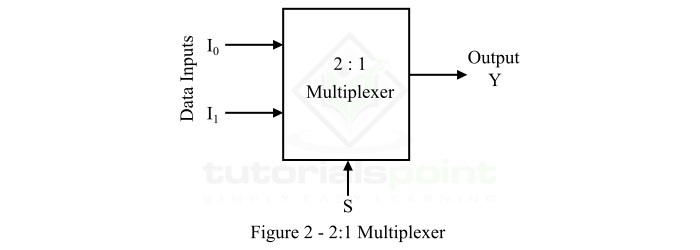
在 2×1 多路复用器中,施加到选择线 S 的数字信号的逻辑电平决定了哪些数据输入将通过输出线。2×1 多路复用器的操作可以从以下真值表中理解。
| 选择线 (S) | 输出 (Y) |
|---|---|
| 0 | I0 |
| 1 | I1 |
4×1 多路复用器
4×1 多路复用器有四个数据输入 I3、I2、I1 和 I0、两条选择线 s1 和 s0 以及一个输出 Y。下图显示了 4×1 多路复用器的框图。
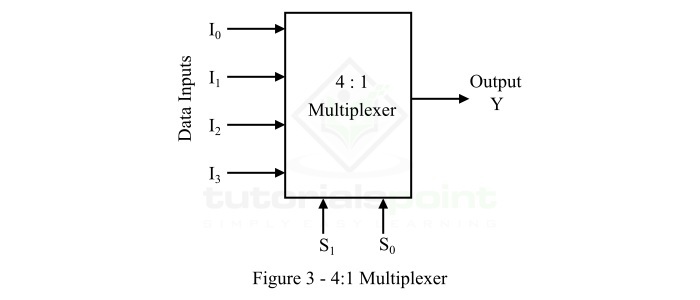
这 4 个输入中的一个将根据这两条选择线上的输入组合连接到输出。 4×1 多路复用器的 真值表 如下所示。
| 选择行 | 输出 | |
|---|---|---|
| S1 | S0 | Y |
| 0 | 0 | I0 |
| 0 | 1 | I1 |
| 1 | 0 | I2 |
| 1 | 1 | I3 |
从真值表,我们可以直接将输出 Y 的布尔函数写为
$$\mathrm{Y\:=\:{S_{1}}'{S_{0}}'I_{0}\:+\:{S_{1}}'S_{0}I_{1}\:+\:S_{1}{S_{0}}'I_{2}\:+\:S_{1}S_{0}I_{3}}$$
我们可以使用反相器、与门和或门来实现这个布尔函数。 4×1 多路复用器的电路图如下图所示。
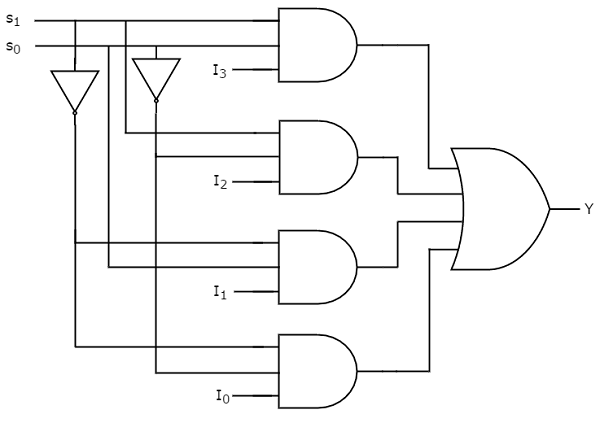
我们可以轻松理解上述电路的运行。类似地,您可以按照相同的步骤实现 8×1 多路复用器和 16×1 多路复用器。
高阶多路复用器的实现
现在,让我们使用低阶多路复用器实现以下两个高阶多路复用器。
- 8×1 多路复用器
- 16×1 多路复用器
8×1 多路复用器
在本节中,让我们使用 4×1 多路复用器和 2×1 多路复用器实现 8×1 多路复用器。我们知道 4×1 多路复用器有 4 个数据输入、2 条选择线和一个输出。而 8×1 多路复用器有 8 个数据输入、3 条选择线和一个输出。
因此,为了获得 8 个数据输入,我们在第一阶段需要两个 4×1 多路复用器。由于每个 4×1 多路复用器产生一个输出,因此在第二阶段,我们需要一个 2×1 多路复用器,将第一阶段的输出视为输入并产生最终输出。
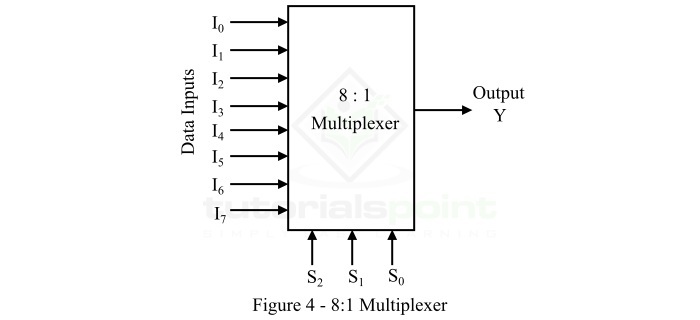
假设 8×1 多路复用器有八个数据输入 I7 至 I0、三条选择线 s2、s1 和s0 和一个输出 Y。8×1 多路复用器的真值表如下所示。
| 选择输入 | 输出 | ||
|---|---|---|---|
| S2 | S1 | S0 | Y |
| 0 | 0 | 0 | I0 |
| 0 | 0 | 1 | I1 |
| 0 | 1 | 0 | I2 |
| 0 | 1 | 1 | I3 |
| 1 | 0 | 0 | I4 |
| 1 | 0 | 1 | I5 |
| 1 | 1 | 0 | I6 |
| 1 | 1 | 1 | I7 |
通过考虑上述真值表,我们可以轻松地使用低阶多路复用器实现 8×1 多路复用器。下图显示了 8×1 多路复用器的框图。
相同的选择线 s1 和 s0 应用于两个 4×1 多路复用器。上部 4×1 多路复用器的数据输入为 I7 至 I4,下部 4×1 多路复用器的数据输入为 I3 至 I0。因此,每个 4×1 多路复用器根据选择线 s1 和 s0 的值产生输出。
第一级 4×1 多路复用器的输出用作第二级 2×1 多路复用器的输入。另一条 选择线 s2 应用于 2×1 多路复用器。
如果 s2 为零,则 2×1 多路复用器的输出将是基于选择线 s1 和 s0 的值的 4 个输入 I3 到 I0 之一s0。
如果 s2 为 1,则 2×1 多路复用器的输出将为 4 个输入 I7 至 I4 之一,具体取决于选择线 s1 和 s0 的值。
因此,两个 4×1 多路复用器和一个 2×1 多路复用器的整体组合相当于一个 8×1 多路复用器。
16×1 多路复用器
在本节中,让我们使用 8×1 多路复用器和 2×1 多路复用器实现 16×1 多路复用器。我们知道 8×1 多路复用器有 8 个数据输入、3 条选择线和一个输出。而 16×1 多路复用器有 16 个数据输入、4 条选择线和一个输出。
因此,为了获得 16 个数据输入,我们在第一阶段需要两个 8×1 多路复用器。由于每个 8×1 多路复用器产生一个输出,因此我们需要在第二阶段使用 2×1 多路复用器,将第一阶段的输出视为输入并产生最终输出。
假设 16×1 多路复用器有 16 个数据输入 I15 至 I0、4 条选择线 s3 至 s0 和一个输出 Y。16×1 多路复用器的真值表如下所示。
| 选择输入 | 输出 | |||
|---|---|---|---|---|
| S3 | S2 | S1 | S0 | Y |
| 0 | 0 | 0 | 0 | I0 |
| 0 | 0 | 0 | 1 | I1 |
| 0 | 0 | 1 | 0 | I2 |
| 0 | 0 | 1 | 1 | I3 |
| 0 | 1 | 0 | 0 | I4 |
| 0 | 1 | 0 | 1 | I5 |
| 0 | 1 | 1 | 0 | I6 |
| 0 | 1 | 1 | 1 | I7 |
| 1 | 0 | 0 | 0 | I8 |
| 1 | 0 | 0 | 1 | I9 |
| 1 | 0 | 1 | 0 | I10 |
| 1 | 0 | 1 | 1 | I11 |
| 1 | 1 | 0 | 0 | I12 |
| 1 | 1 | 0 | 1 | I13 |
| 1 | 1 | 1 | 0 | I14 |
| 1 | 1 | 1 | 1 | I15 |
通过考虑上述真值表,我们可以轻松地使用低阶多路复用器实现 16×1 多路复用器。下图显示了 16×1 多路复用器的框图。
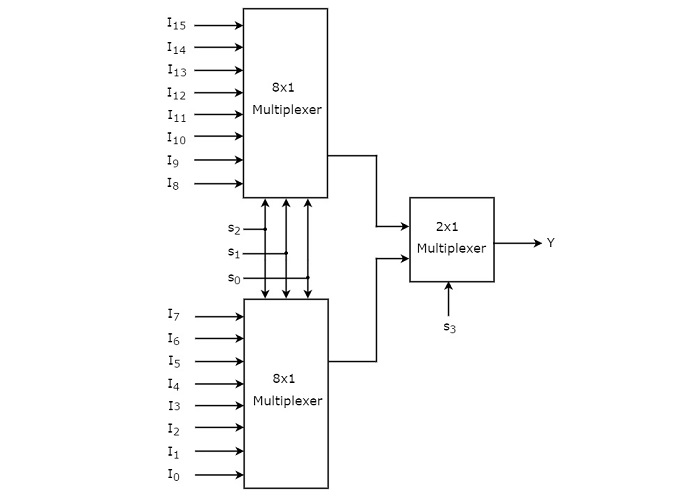
两个 8×1 多路复用器均应用了相同的选择线 s2、s1 和 s0。上 8×1 多路复用器的数据输入为 I15 至 I8,下 8×1 多路复用器的数据输入为 I7 至 I0。因此,每个 8×1 多路复用器根据选择线 s2、s1 和 s0 的值产生输出。
第一级 8×1 多路复用器的输出用作第二级 2×1 多路复用器的输入。另一条 选择线 s3 应用于 2×1 多路复用器。
如果 s3 为零,则 2×1 多路复用器的输出将是基于选择线 s2、s1 和 s0 的值的 8 个输入 Is7 至 I0 之一。 s0。
如果 s3 为 1,则 2×1 多路复用器的输出将为 8 个输入 I15 至 I8 中的一个,具体取决于选择线 s2、s1 和 s0 的值。
因此,两个 8×1 多路复用器和一个 2×1 多路复用器的整体组合相当于一个 16×1 多路复用器。
多路复用器的应用
在数字电子技术中,多路复用器在几乎所有类型的数字系统中都有广泛的应用。多路复用器的一些重要应用如下 −
- 数据路由和数据选择
- 并行到串行转换
- 逻辑功能实现
- 波形生成等
结论
在本教程中,我们详细讨论了数字电子中使用的不同类型的多路复用器及其功能和应用。


