通过 NAND 门实现 XNOR 门
众所周知,NAND 门是一种通用逻辑门,使用它我们可以实现任何其他类型的逻辑门或逻辑表达式。阅读本教程以了解如何仅使用 NAND 门实现 XNOR 门。让我们从 XNOR 和 NAND 门的基本概述开始。
什么是 XNOR 门?
XNOR(异或非)门是一种派生逻辑门。XNOR 门是一种具有两个输入和一个输出的逻辑门。当 XNOR 门的两个输入相等时,即高电平(逻辑 1)或低电平(逻辑 0),XNOR 门会产生高电平(逻辑 1)输出。
当 XNOR 门的两个输入不同时,即一个为高电平(逻辑 1),另一个为低电平(逻辑 0),则 XNOR 门的输出为低电平(逻辑 0)状态。XNOR 门的逻辑符号如图 1 所示。

因此,仅当 XNOR 门的两个输入相等时,XNOR 门才会产生高电平(逻辑 1)输出。因此,XNOR 门也被称为"相等检测器"。
XNOR 门的输出由以下公式给出:
$$\mathrm{Y \: = \: A \odot B \: = \: AB \: + \: \bar{A} \: \bar{B}}$$
其中,A 和 B 是 XNOR 门的两个输入变量,Y 是 XNOR 门的输出变量。XNOR 门的输出表达式为 Y 等于 A ex-nor B。
XNOR 门的真值表
真值表显示了 XNOR 门的输入和输出之间的关系。 XNOR 门的真值表如下所示。
| 输入 | 输出 | |
|---|---|---|
| A | B | Y = (AB + A'B') |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
什么是 NAND 门?
NAND 门是一种通用逻辑门。通用逻辑门可用于实现任何类型的逻辑表达式或任何其他类型的逻辑门。
NAND 门基本上是两种基本逻辑门的组合,即 AND 门和非门,即
$$\mathrm{NAND \: Logic \: = \: AND \:Logic \: + \: NOT \: Logic}$$
NAND 门是一种逻辑门,当其所有输入都为高电平时,输出为低电平(逻辑 0),当其任何输入为低电平(逻辑 0)时,输出为高电平(逻辑 1)。因此,NAND 门的操作与 AND 门的操作相反。图 2 显示了双输入 NAND 门的逻辑符号。

NAND 门的输出方程
如果 A 和 B 是输入变量,Y 是 NAND 门的输出变量,则其输出由以下公式给出:
$$\mathrm{Y \: = \: \overline{A \cdot B} \: = \: (A \cdot B)'}$$
读作 "Y is equal to A·B whole bar"。
NAND 真值表门
以下是 NAND 门的真值表 −
| 输入 | 输出 | |
|---|---|---|
| A | B | Y = (A·B)' |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
现在,让我们讨论如何从 NAND 门实现 XNOR 门。
从 NAND 门实现 XNOR 门
如上所述,NAND 门是一种通用逻辑,我们可以使用它实现任何其他类型的逻辑门。使用 NAND 门实现 XNOR 门如图 3 所示。
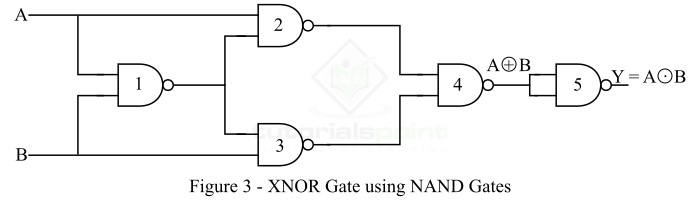
从仅使用 NAND 门的 XNOR 门的逻辑电路图中可以看出,我们需要 5 个 NAND 门。
现在,让我们了解这个 NAND 逻辑电路如何产生与 XNOR 门相当的输出 −
第一个 NAND 门的输出是,
$$\mathrm{Y_{1} \: = \: \overline{A \: B}}$$
第二和第三个 NAND 门的输出是,
$$\mathrm{Y_{2} \: = \: \overline{A \cdot \: \overline{AB}}}$$
$$\mathrm{Y_{3} \: = \: \overline{B \cdot \: \overline{AB}}}$$
这两个输出(Y2 和 Y3)连接到第四个 NAND 门。这个 NAND 门将产生一个输出,
$$\mathrm{Y \: = \: \overline{\overline{A \cdot \: \overline{AB}} \cdot \overline{B \cdot \overline{AB}}}}$$
$$\mathrm{\Rightarrow \: Y \: = \: A \cdot \overline{AB} \: + \: B \cdot \overline{AB} \: = \: A(\bar{A} \: + \: \bar{B}) \: + \: B(\bar{A} \: + \: \bar{B})}$$
$$\mathrm{\Rightarrow \: Y \: = \: A \: \bar{A} \: + \: A \: \bar{B} \: + \: \bar{A} \: B \: + \: B \: \bar{B}}$$
$$\mathrm{\therefore \: Y \: = \: A \: \bar{B} \: + \: \bar{A} \:B \: = \: A \oplus B}$$
最后,第四个 NAND 门的输出被输入到第五个 NAND 门,后者起反相器的作用,产生一个与 XNOR 门等价的输出,即
$$\mathrm{Y \: = \: \overline{A \oplus B} \: = \: A \odot B}$$
这就是 XNOR 门的输出。因此,这样,我们就可以仅用 NAND 门来实现 XNOR 门。


