带 NAND 门的全加器
在数字电子技术中,有不同类型的逻辑电路用于执行不同类型的算术运算。其中之一就是加法器。加法器(或二进制加法器)是一种组合逻辑电路,可执行两个或多个二进制数的加法并给出输出和。有两种类型的加法器,即半加法器和全加法器。
由于加法器是逻辑电路,因此它们是使用不同类型的数字逻辑门实现的,例如或门、与门、非门、与非门、或非门等。在这里,我们将讨论使用与非门实现全加器。但在此之前,让我们先了解一下全加器的基础知识。
什么是全加器?
可以将两个二进制数字(位)和一个进位相加,并产生一个和位和一个进位作为输出的组合逻辑电路称为全加器。换句话说,设计用于添加三个二进制数字并产生两个输出(和和进位)的组合电路称为全加器。因此,全加器电路将三个二进制数字相加,其中两个是输入,一个是从上一次加法转发的进位。全加器的框图如图 1 所示。
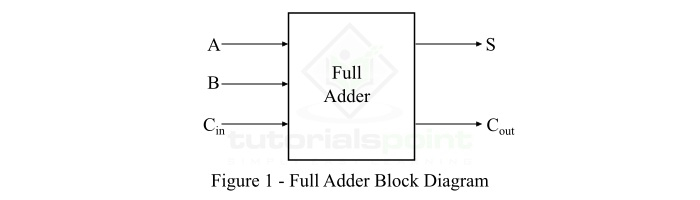
从全加器的框图中可以清楚地看出,它有三个输入,即 A、B、Cin。其中,A 和 B 是输入位,Cin 是来自前一级的进位位。它有两个输出变量,即总和 (S) 和进位 (Cout)。
全加器真值表
以下是全加器电路的真值表 −
| 输入 | 输出 | |||
|---|---|---|---|---|
| A | B | Cin | S (Sum) | Cout (Carry) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
因此,从真值表可知,当只有1个输入等于1或所有输入都等于1时,全加器的和输出等于1。而当两个或三个输入等于1时,进位输出的进位为1。
全加器的输出方程可以从全加器的真值表中获得。这些方程如下 −
总和输出
$$\mathrm{Sum,\, S=A'B'C_{in}+A'BC'_{in}+AB'C'_{in}+ABC_{in}=A\oplus B\oplus C_{in} }$$
进位输出
$$\mathrm{Carry,\, C_{out}=AB+AC_{in}+BC_{in}}$$
现在,让我们讨论使用 NAND 门实现全加器。
使用 NAND 门的全加器
全加器电路可以使用 NAND 逻辑门实现,如图 2 所示。
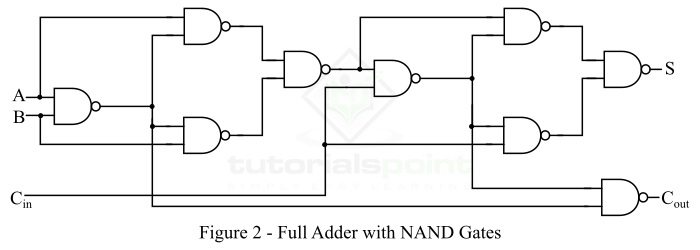
从使用 NAND 门的全加器的逻辑电路图中可以看出,全加器需要 9 个 NAND 门。
带 NAND 门的全加器电路的和输出方程如下 −
$$\mathrm{S=\overline{\overline{\left ( A\oplus B ight )\cdot \overline{\left ( A\oplus B ight )C_{in}}}\cdot \overline{C_{in}\cdot\overline{\left ( A\oplus B ight )C_{in}}} }=A\oplus B\oplus C_{in}}$$
其中,
$$\mathrm{A\oplus B=\overline{\overline{A\cdot \overline{AB}}\cdot \overline{B\cdot \overline{AB}}}}$$
带有 NAND 门的全加器电路的进位输出方程为,
$$\mathrm{C_{out}=\overline{\overline{C_{in}\left ( A\oplus B ight )}\cdot \overline{AB}}=AB+\left ( A\oplus B ight )C_{in}}$$
这样,我们就可以仅使用 NAND 门来实现全加器电路。


