多路复用器设计过程和应用
多路复用器 (MUX) 是一种数字组合逻辑电路,它接受多个数据输入,但每次只允许其中一个数据通过输出通道传输。多路复用器由 2n 条输入线、n 条选择线和一条输出线组成。在多路复用器中,所需数据输入到输出通道的路由由应用于选择线的逻辑电平完成。多路复用器的功能框图如图 1 所示。
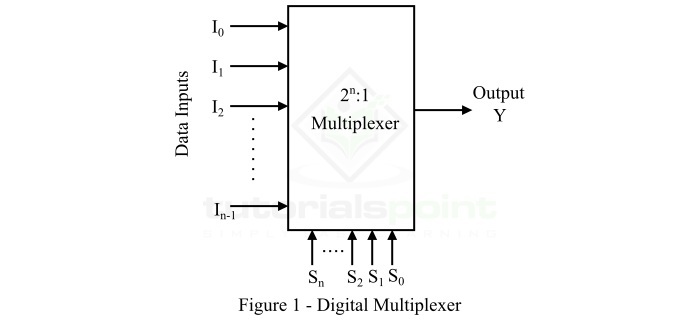
本章主要用于解释不同类型的多路复用器电路的设计过程。更具体地说,我们将在这里讨论以下三种多路复用器的设计过程 −
- 2:1 多路复用器
- 4:1 多路复用器
- 8:1 多路复用器
现在让我们讨论这三种多路复用器的设计。
设计 2:1 多路复用器
2:1 多路复用器 (MUX) 具有 2 条输入线 (I0 和 I1)、1 条选择线 (S) 和 1 条输出线 (Y)。施加到选择线 S 的逻辑电平决定了哪些数据输入将通过输出线。
为了确定 2:1 多路复用器的输出 (Y) 的布尔表达式及其逻辑电路实现,我们首先需要其函数表(真值表),该表提供有关电路操作的信息。数据输入为 I0 和 I1 的 2:1 多路复用器的功能表如下所示。
| 选择线 (S) | 输出 (Y) |
|---|---|
| 0 | I0 |
| 1 | I1 |
利用此真值表,我们可以写出 2:1 MUX 输出的逻辑表达式如,
$$\mathrm{Y\:=\:\bar{S}I_{0} \: + \: SI_{1}}$$
要实现此逻辑表达式,我们需要两个与门、一个非门和一个或门。2:1 MUX 的逻辑电路如图 2 所示。
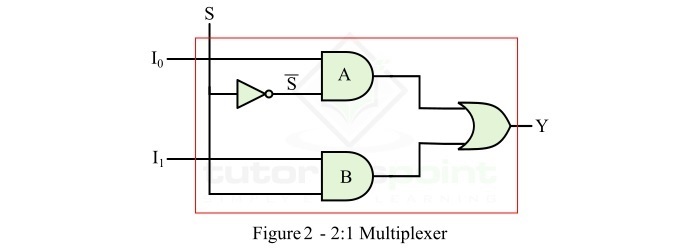
操作
图 2 所示的 2:1 MUX 的逻辑电路将按如下方式工作 −
- 当 S = 0 时,AND 门 A 启用,AND 门 B 禁用。因此,输出 Y = I0。
- 当 S = 1 时,AND 门 A 禁用,AND 门 B 启用。因此,输出 Y = I1。
这就是我们设计 2:1 多路复用器的方法。
设计 4:1 多路复用器
4:1 多路复用器 (MUX) 是具有 4 条输入线 (I0、I1、I2 和 I3)、2 条选择线 (S0 和 S1) 和 1 条输出线 (Y) 的 MUX。应用于选择线 S0 和 S1 的逻辑电平决定了哪个数据输入将传输到输出线。
为了确定 4:1 多路复用器及其逻辑电路的输出 (Y) 的布尔表达式,我们需要其函数表(真值表),该表提供有关其电路操作的信息。数据输入为 I0、I1、I2 和 I3 的 4:1 多路复用器的功能表如下。
| 选择行 | 输出 (Y) | |
|---|---|---|
| S1 | S0 | |
| 0 | 0 | I0 |
| 0 | 0 | I1 |
| 1 | 0 | I2 |
| 1 | 1 | I3 |
利用这个真值表,我们可以写出 4:1 MUX 输出的逻辑表达式如,
$$\mathrm{Y=\bar{S_{1}}\bar{S_{0}}I_{0}+\bar{S_{1}}S_{0}I_{1}+S_{1}\bar{S_{0}}I_{2}+S_{1}S_{0}I_{3}}$$
要实现这个逻辑表达式,我们需要四个与门、两个非门和一个或门。因此,4:1 MUX 的逻辑电路如图 3 所示。
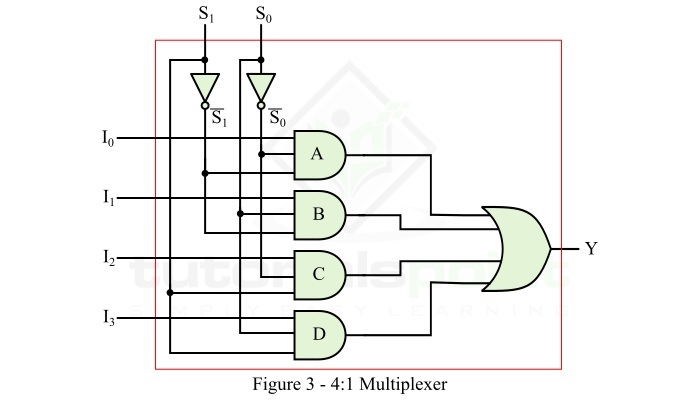
操作
图 3 所示的 4:1 MUX 的逻辑电路将按以下方式工作 −
- 当 S1 = 0 且 S0 = 0 时,AND 门 A 启用,AND 门 B、C 和 D 禁用。因此,输出 Y = I0。
- 当 S1 = 0 且 S0 = 1 时,AND 门 B 启用,AND 门 A、C 和 D 禁用。因此,输出 Y = I1。
- 当 S1 = 1 且 S0 = 0 时,AND 门 C 启用,AND 门 A、B 和 D 禁用。因此,输出 Y = I2。
- 当 S1 = 1 且 S0 = 1 时,AND 门 D 启用,AND 门 A、B 和 C 禁用。因此,输出 Y = I3。
这样,我们可以设计一个 4:1 多路复用器。
设计 8:1 多路复用器
8:1 多路复用器 (MUX) 是一个组合逻辑电路,具有 8 条输入线 (I0、I1、I2、I3、I4、I5、I6 和 I7)、3 条选择线 (S0、S1 和 S2) 和 1 条输出线 (Y)。应用于选择线 S0、S1 和 S2 的逻辑电平决定哪些数据输入将传输到输出线。
为了确定 8:1 多路复用器及其逻辑电路的输出 (Y) 的逻辑表达式,我们需要其功能表(真值表),该表提供有关其逻辑电路操作的信息。
下面给出了具有数据输入 I0、I1、I2、I3、I4、I5、I6 和 I7 以及选择线 S0、S1 和 S2 的 8:1 多路复用器的功能表。
| 选择行 | 输出 (Y) | ||
|---|---|---|---|
| S2 | S1 | S0 | |
| 0 | 0 | 0 | I0 |
| 0 | 0 | 1 | I1 |
| 0 | 1 | 0 | I2 |
| 0 | 1 | 1 | I3 |
| 1 | 0 | 0 | I4 |
| 1 | 0 | 1 | I5 |
| 1 | 1 | 0 | I6 |
| 1 | 1 | 1 | I7 |
通过使用此函数表,我们可以写出8:1 MUX输出的逻辑表达式如,
$$\mathrm{Y\:=\:\bar{S_{2}}\bar{S_{1}}\bar{S_{0}}I_{0}+\bar{S_{2}}\bar{S_{1}}S_{0}I_{1}+\bar{S_{2}}S_{1}\bar{S_{0}}I_{2}+\bar{S_{2}}S_{1}S_{0}I_{3}+S_{2}\bar{S_{1}}\bar{S_{0}}I_{4}+S_{2}\bar{S_{1}}S_{0}I_{5}+S_{2}S_{1}\bar{S_{0}}I_{6}+S_{2}S_{1}S_{0}I_{7}}$$
要实现这个逻辑表达式,我们需要八个与门,三个非门和一个或门。因此,8:1 MUX 的逻辑电路如图 4 所示。
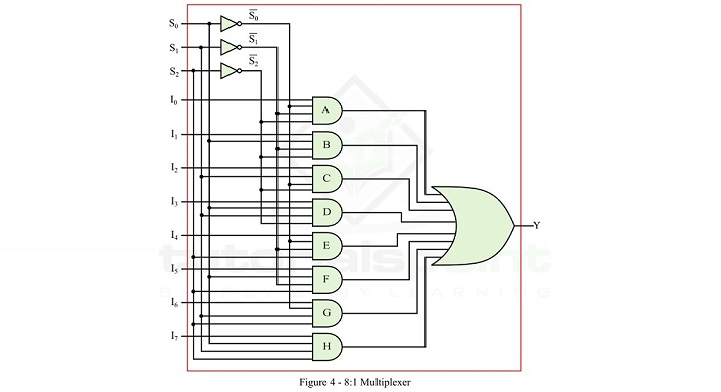
操作
图 4 所示的 8:1 MUX 的逻辑电路将按如下方式运行 −
- 当 S2 = 0、S1 = 0 且 S0 = 0 时,与门 A 被启用,而逻辑电路中的所有其他与门都被禁用。因此,输出 Y = I0。
- 当 S2 = 0、S1 = 0 且 S0 = 1 时,与门 B 被启用,而逻辑电路中的所有其他与门都被禁用。因此,输出 Y = I1。
- 当 S2 = 0、S1 = 1 且 S0 = 0 时,与门 C 被启用,而逻辑电路中的所有其他与门都被禁用。因此,输出 Y = I2。
- 当 S2 = 0、S1 = 1 且 S0 = 1 时,与门 D 被启用,而逻辑电路中的所有其他与门均被禁用。因此,输出 Y = I3。
- 当 S2 = 1、S1 = 0 且 S0 = 0 时,与门 E 被启用,而逻辑电路中的所有其他与门均被禁用。因此,输出 Y = I4。
- 当 S2 = 1、S1 = 0 且 S0 = 1 时,与门 F 被启用,而逻辑电路中的所有其他与门均被禁用。因此,输出 Y = I5。
- 当 S2 = 1、S1 = 1 且 S0 = 0 时,与门 G 被启用,逻辑电路中所有其他与门均被禁用。因此,输出 Y = I6。
- 当 S2 = 1、S1 = 1 且 S0 = 1 时,与门 H 被启用,逻辑电路中所有其他与门均被禁用。因此,输出 Y = I7。
这样,我们可以设计一个 8:1 多路复用器。
多路复用器的应用
多路复用器是数字系统中广泛使用的组合逻辑电路之一。下面列出了多路复用器的一些重要应用。
- 多路复用器用作数据选择器。
- 多路复用器用于通信系统以提高系统效率。
- 多路复用器用于电话网络,用于在一条传输线上集成多个音频信号。
- 为了保存大量数据,多路复用器也用于计算机内存系统。
- 多路复用器也用于电视广播系统。
- 多路复用器用于卫星通信和 GPS(全球定位系统)。
- 多路复用器还用于 PLC(可编程逻辑控制)系统等。
这都是关于多路复用器的设计过程,以及多路复用器的应用。


