数字电子技术 - 布尔函数
在数字电子技术中,布尔函数是一个基本概念,它定义了输入二进制变量和二进制结果之间的逻辑和数学关系。这些函数是根据布尔代数和二进制数字系统的规则定义的。
在本章中,我们将解释布尔函数的基础知识、它们的属性、优点和应用。那么,让我们从布尔函数的基本介绍开始吧。
什么是布尔函数?
布尔函数是一个由二进制变量和逻辑运算符组成的数学表达式。它定义了二进制变量和二进制输出之间的逻辑关系。
布尔函数是使用布尔代数和二进制数字系统的规则定义的。这些函数构成了数字电路和系统设计和开发的基础。
布尔函数的组成部分
布尔函数由以下两个主要组成部分组成 −
- 二进制变量
- 逻辑运算符
二进制变量
二进制变量是一个可以取两个可能值之一的符号,即 0 和 1。如果二进制变量具有与之关联的值 0。那么它代表低或假状态。而如果二进制变量的值为 1,则它代表高或真状态。
逻辑运算符
逻辑运算符是一个表示逻辑运算或过程的符号。在布尔代数中,有三个基本逻辑运算符 −
AND 运算符
用点 (.) 表示。AND 运算的输出为真或高或逻辑 1,当且仅当其所有输入变量的值均为真或高或逻辑 1。它是一个二元运算符,因为它至少需要两个输入变量。
OR 运算符
用加号 (+) 表示。它也是一个二元运算符,因为至少需要两个输入变量。如果 OR 运算的任何输入为真或高或逻辑 1,则其输出为真或高或逻辑 1。
NOT 运算符
NOT 运算符用波浪符号 (~) 表示。它是一个一元运算符,只需要一个输入变量。NOT 运算符反转或补充输入变量的值。因此,如果输入变量的值为 1,则输出为 0,反之亦然。
布尔函数的表示
布尔函数可以表示为几种不同的形式。以下是一些常用的布尔函数表示形式 −
数学形式
在这种形式中,布尔表达式表示为由二进制变量和逻辑运算符组成的数学表达式,这些符号形式。例如,
Y(A,B,C) = AB + ABC + BC
这种形式也称为代数形式。
真值表
在这种形式中,布尔函数以表格格式表示。该表表示了布尔函数的二进制变量及其对应的二进制输出的所有可能组合。
例如,Y = A + B 是一个布尔函数,其真值表表示如下所示。
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
逻辑电路图
它是布尔函数的图形表示。逻辑电路图通过逻辑门的互连来表示布尔函数。其中,每个逻辑门都使用其符号表示。
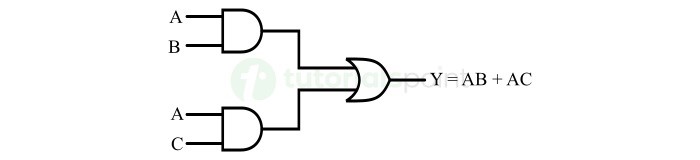
布尔函数 Y = AB + AC 的逻辑电路图如下图所示。
布尔函数在数字电子技术中的重要性
在数字电子技术中,布尔函数是用于表达不同变量和输出值之间的逻辑关系的关键概念。我们知道,数字系统使用二进制信息,其中二进制信息使用二进制变量来表示。
布尔函数提供了一种高效且合乎逻辑的方式来表达这些二进制变量之间的关系,以便系统可以理解和操纵二进制信息。
布尔函数还为逻辑门和其他数字电路的设计提供了基础。基本上,它们提供了一种系统的数学方法来设计和分析数字系统。
我们还可以使用布尔函数来理解和验证数字电路对不同可能输入的行为。因此,布尔函数也被用作数字系统的调试和优化工具。
总体而言,布尔函数是数字电子领域中用于执行各种任务的标准化工具,例如数字电路和系统操作的实现、分析、优化和验证。
布尔函数的特征
布尔函数具有几个重要特征,使其成为设计、实现和分析数字电路的重要工具。布尔函数的一些主要特征列于下方 −
- 布尔函数提供了一种简单明了的方法来表达数字系统的输入变量和输出之间的逻辑关系。
- 布尔函数可用作了解数字电路对不同输入组合的行为的工具。
- 布尔函数由二进制变量组成。因此,它们可以直接使用逻辑门实现。
- 布尔函数也有助于确定数字系统的输出,而无需实际实现。
- 布尔函数在降低系统复杂性和降低成本方面也发挥着至关重要的作用。
- 布尔函数允许检测和纠正数字系统设计中的错误,以提高准确性和可靠性。
所有这些都是布尔函数的重要特征。除了这些优点之外,布尔函数还有几个限制,将在下一节中列出。
布尔函数的局限性
以下是布尔函数的一些主要限制的列表 −
- 布尔函数依赖于二进制数字系统。因此,它们不适合表示数字电子领域之外的许多问题。
- 布尔函数对输入值的微小变化非常敏感。这种高敏感性有时会产生不可预测的结果。
- 布尔函数不能直接表达自然的算术运算。
- 布尔函数对于统计建模等某些应用并不方便。
布尔函数的应用
布尔函数在数字电子技术和计算机科学领域有着广泛的应用。
下面介绍了布尔函数的一些关键应用 −
- 布尔函数用于设计、分析和实现数字电路。
- 计算机系统和微处理器的设计和操作是通过布尔函数定义的。
- 布尔函数还用于表达逻辑门、触发器、计数器、解码器和所有其他数字系统的输出。
- 布尔函数还用于设计用于数字信号处理。
- 布尔函数用于电气和电子工程,以设计、实施和分析控制系统、自动化系统等。
结论
总之,布尔函数是一种基本工具,用于指定二进制变量与数字系统输出之间的系统、数学和逻辑关系。
布尔函数用途广泛,可用于数字系统的设计、分析、实施、优化等各种目的。


