使用 NOR 门实现 AND 门
AND 门是一种执行二进制乘法的基本逻辑门,即,只有当其所有输入都处于 HIGH 或逻辑 1 状态时,它才会产生 HIGH 或逻辑 1 输出。另一方面,NOR 门是一种通用逻辑门。因此,NOR 门可用于实现任何其他类型的逻辑门。
在仅使用 NOR 门实现 AND 门之前,让我们先讨论一下 AND 门和 NOR 门的基本理论。
什么是 AND 门?
AND 门是一种基本逻辑门。AND 门可能有两个或两个以上的输入,但只提供一个输出。如果 AND 门的任何一个输入处于 LOW 或逻辑 0 状态,则输出 LOW(逻辑 0),否则输出 HIGH(逻辑 1)。因此,只有当 AND 门的所有输入都处于 HIGH 或逻辑 1 状态时,其输出才会是 HIGH 或逻辑 1 状态。
AND 门也称为"全有或全无门"。图 1 显示了双输入与门的逻辑符号。

如果变量 A 和 B 是与门的输入,Y 是与门的输出变量,则与门的输出方程为:
$$\mathrm{Y \: = \: A\cdot B}$$
其中,"." (点) 符号表示与运算。读作"Y 等于 A AND B"。
与门的真值表
显示与门的输入和输出之间关系的表称为与门的真值表。以下是与门的真值表 −
| 输入 | 输出 | |
|---|---|---|
| A | B | Y = A · B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
什么是 NOR 门?
NOR 门是一种通用逻辑门,因为这种逻辑门可用于实现任何其他类型的逻辑门。
NOR 表示 NOT + OR。这意味着,OR 输出被 NOT 或反转。因此,NOR 门是 OR 门和非门的组合,即
$$\mathrm{NOR \: Gate \: = \: OR \: Gate \: + \: NOT \: Gate}$$
NOR 门是一种逻辑门,只有当其所有输入都为 LOW(逻辑 0)时,其输出才为 HIGH(逻辑 1),即使其任何输入变为 HIGH(逻辑 1),其输出也为 LOW(逻辑 0)。图 2 显示了双输入 NOR 门的逻辑符号。

如果变量 A 和 B 是 NOR 门的输入变量,Y 是 NOR 门的输出变量,则 NOR 门的输出由以下公式给出:
$$\mathrm{Y \: = \: \overline{A \: + \: B} \: = \: (A \: + \: B)'}$$
读作 "Y is equal to A plus B whole bar"
NOR 门的真值表
以下是 NOR 门的真值表或非门 −
| 输入 | 输出 | |
|---|---|---|
| A | B | Y = A · B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
现在,让我们讨论如何从 NOR 门实现 AND 门。
从 NOR 门实现 AND 门
如上所述,NOR 门是逻辑门,因此,我们可以使用它来实现 AND 门。图 3 仅显示了从 NOR 门实现 AND 门。
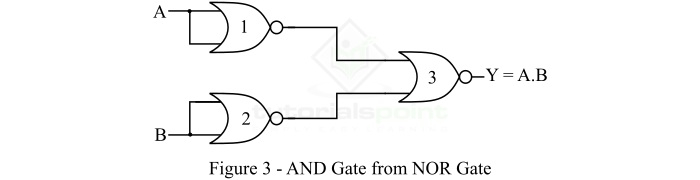
因此,要从 NOR 门实现 AND 门,我们需要 3 个 NOR 门。其中,前两个或非门用于对输入变量A和B进行补码,第三个或非门用于产生与AND运算等价的输出。
输出方程
前两个或非门的输出为,
$$\mathrm{Y_{1} \: = \: \bar{A}}$$
$$\mathrm{Y_{2} \: = \: \bar{B}}$$
第三个或非门的输出为,
$$\mathrm{Y \: = \: \overline{\bar{A} \: + \: \bar{B}} \: = \: \bar{\bar{A}} \cdot \bar{\bar{B}} \: = \: A \cdot B} $$
这是 AND 门的输出。因此,图 3 中所示的使用 NOR 门的逻辑电路等同于 AND 门。


