数字电子技术 - 八进制算术
什么是八进制算术?
在数字电子技术中,八进制数广泛用于系统设计、编码、解码等。八进制算术可以定义为提供一组规则和运算符来操作八进制数的数学。换句话说,使用八进制数进行数值计算的数学系统称为八进制算术。
在八进制算术中,我们可以执行以下四个基本算术运算 −
- 八进制加法
- 八进制减法
- 八进制乘法
- 八进制除法
在数字电子系统中,八进制数用于以更紧凑的形式表示二进制信息和数据,因为八进制数字可以表示一组三个二进制数字或位。因此,在数字电子技术研究中,理解八进制算术非常重要。
让我们借助示例逐一详细讨论四种八进制算术运算。
八进制加法
在八进制算术中,八进制加法是用于将两个或多个八进制数相加以得出其和的基本算术运算之一。八进制加法类似于十进制加法。但是,在八进制加法的情况下,当总和等于或大于 8 时,会产生进位以传递到下一列。
让我们看一些已解决的示例来了解八进制加法的过程。
示例 1
添加 (315)8 和 (222)8。
解决方案
八进制数 315 和 222 的加法如下所示 −
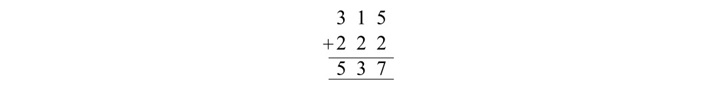
解释
将最右边一列的八进制数字相加:5 + 2 = 7。记下数字 7 作为结果。
移至第二列,将八进制数字 1 和 2 相加:1 + 2 = 3。记下数字 3 作为结果。
移至下一列,将第三列中的八进制数字相加:3 + 2 = 5。记下数字 5 作为结果。
因此,315 和 222 的八进制加法的最终结果是 537。
示例 2
执行八进制加法 (372)8 + (716)8。
解决方案
下面解释了给定八进制数的加法 −

解释
将最右列的八进制数字相加:2 + 6 = (10)8。因此,记下最后一位数字 (0) 作为结果,并将 1 进位到下一列。
移至第二列,并将包括上一步进位的八进制数字相加:7 + 1 + 1 = (11)8。将最后一位数字 (1) 作为结果,并将左边的 1 进位到下一列。
移至第三列,将八进制数字与上一步的进位相加:3 + 7 + 1 = 13。没有剩余数字可加。因此,记下结果。
因此,八进制加法的最终结果是 1310。
八进制减法
八进制减法是另一种对八进制数执行的基本算术运算。它用于查找两个八进制数之间的差值。
假设八进制减法为 (x)8 - (y)8,如果数字 x 小于数字 y,则从下一个高阶位置借位 1 来执行八进制减法。
让我们看一些已解决的例子来理解八进制减法。
示例 1
从 (325)8 中减去 (213)8。
解决方案
给定的八进制减法在下方执行 −
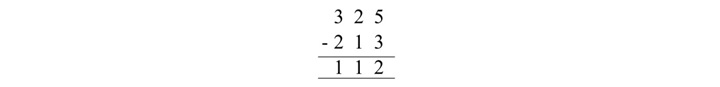
解释
从最右列的数字开始减法:5 – 3 = 2。记下数字 2 作为结果。
移至下一列并减去数字:2 – 1 = 1。记下数字作为结果。
移至下一列并减去八进制数字:3 – 2 = 1。记下数字 1 作为结果。
因此,给定八进制减法的最终结果是 (112)8。
示例2
从 (317)8 中减去 (125)8。
解决方案
数字 3178 和 1258 的八进制减法解释如下 −

解释
减去最右边的数字:7 – 5 = 2。记下数字 2 作为结果。
移至第二列并减去数字:1 – 2。由于 1 小于 2,因此从下一个更高的数字借位 1,使其变为 11。因此,八进制减法是11 – 2 = 7。记下八进制数字 7 作为结果。
移至最左边的列并减去数字:2 – 1 = 1。记下数字 1 作为结果。
因此,减法的最终结果是 (172)8。
八进制乘法
八进制乘法是针对八进制数执行的第三个基本算术运算。它用于求两个八进制数的乘积。
八进制乘法是通过将一个八进制数的每个数字乘以另一个八进制数的每个数字来执行的。最终结果通过对乘法的所有部分乘积求和得到。
以下数值示例演示了执行八进制乘法的方法。
示例 1
将 (375)8 乘以 (5)8。
解决方案
下面解释了给定八进制数的乘法 −

解释
将八进制数字 5 乘以八进制数 375 的每个数字。写下乘法结果以获得最终乘积,即 (2361)8。
示例 2
对 (624)8 和 (25)8 进行八进制乘法。
解决方案
给定八进制数的乘法解释如下 −

解释
将第二个八进制数 25 的最右边数字 (5)8 乘以第一个八进制数 624 的每个数字,并记下部分积。
移动到八进制数 25 的下一个数字 (2)8 并将其乘以八进制数的每个数字624. 向左移动一位并记下部分积。
将所有部分积相加,得到最终结果,即 (20444)8。
八进制除法
八进制除法是可以对八进制数执行的基本算术运算之一,用于求出它们的商和余数。
八进制除法的分步过程如下 −
步骤 1 − 首先将被除数的最左边的数字除以除数。
步骤 2 − 将除数得到的商相乘,并从被除数中减去乘积。
步骤 3 −将被除数的下一个八进制数字放下来,并重复上述两个步骤,直到被除数中的所有数字都用完为止。
让我们通过一些已解决的示例来了解八进制数的除法。
示例 1
将 (1275)8 除以 (3)8。
解决方案
给定数字的八进制除法如下所示 −
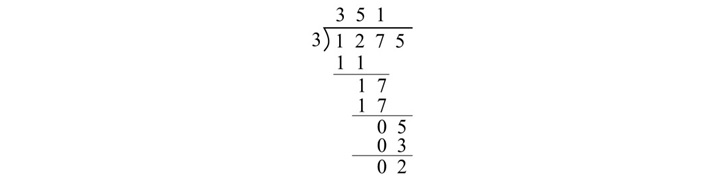
在此示例中,将八进制数 (1275)8 除以 (3)8 可得出 (351)8 作为商,将 (2)8 作为余数。
让我们再举一个例子来更好地理解八进制除法。
示例 2
对 (1365)8 进行八进制除法,除以 (5)8。
解决方案
给定数字的八进制除法如下所示 −
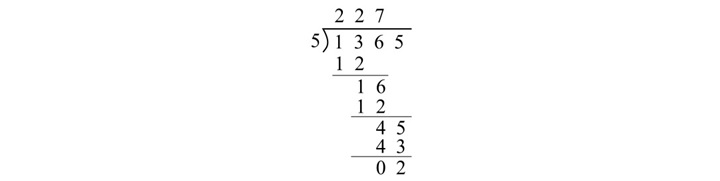
在此八进制除法示例中,商为 (227)8,余数为 (2)8。
我们还可以通过将其转换为二进制形式来执行八进制算术运算。我们知道,一个八进制数字可以用一组 3 个二进制数字或位来表示。
下表给出了每个八进制数字的二进制表示形式 −
| 八进制数字 | 3 位二进制 |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
让我们看一些例子来学习通过二进制转换进行八进制算术运算。
通过二进制转换进行八进制加法
通过二进制转换将两个八进制数相加可以按照以下步骤进行 −
步骤 1 − 将给定的八进制数转换为其二进制等价数。
步骤 2 − 将获得的二进制数相加。
步骤 3 −将最终结果转换回八进制格式。
示例
通过二进制转换将 (75)8 和 (14)8 相加。
解决方案
将给定的八进制数转换为其二进制等价数。
(75)8 = (111 101)2
(14)8 = (001 100)2
以二进制格式添加八进制数,

将二进制和转换为八进制以获得最终结果,
(001 001 001)2 = (111)8
通过二进制转换进行八进制减法
要通过二进制转换对两个数字进行八进制减法,我们首先将它们转换为它们的二进制等价数,然后根据二进制减法规则进行减法,最后将最终结果转换回八进制数系统。
以下是一个例子,演示了如何通过二进制转换进行八进制减法。
示例
通过二进制转换从 (47)8 中减去 (16))8等价的。
解决方案
将给定的八进制数转换为其等价的二进制数,
(47)8 = (100 111)2
(16)8 = (001 110)2
使用二进制减法规则减去数字,

将结果转换回八进制数系统,
(011 001)2 = (31)8
通过二进制转换进行八进制乘法
就像加法和减法一样,我们也可以通过将八进制数转换为等效的二进制数来执行八进制数的乘法。以下示例演示了如何通过二进制转换执行八进制乘法。
示例
以二进制形式将 (417)8 乘以 (3)8。
解决方案
将给定的八进制数转换为二进制,
(417)8 = (100 001 111)2
(3)8 = (011)2
将获得的二进制数相乘,

将结果转换回八进制格式,
(1 100 101 101)2 = (1455)8
通过二进制转换进行八进制除法
要通过二进制转换进行八进制除法,我们首先将给定的八进制数转换为其等效的二进制数,然后按照二进制除法的规则执行除法,最后将结果转换回八进制形式。
以下示例说明如何通过二进制转换进行八进制除法。
示例
使用二进制转换方法将 (547)8 除以 (5)8。
解决方案
将给定的八进制数转换为其二进制数等价,
(547)8 = (101 100 111)2
(5)8 = (101)2
按照二进制除法算术规则执行二进制除法,
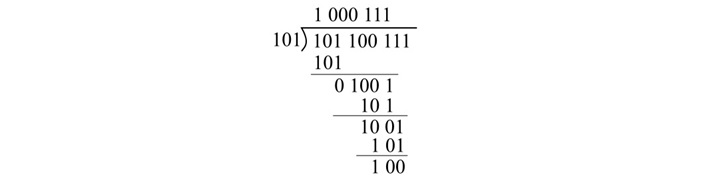
将二进制结果转换回八进制格式,
商 = (1 000 111)2 = (107)8
余数 = (100)2 = (4)8
结论
在本章中,我们解释了八进制数的各种算术运算,例如加法、减法、乘法和除法。
我们还介绍了八进制算术运算的二进制方法,其中我们首先将给定的八进制数转换为其二进制等价数,然后执行算术运算,最后将二进制结果转换回八进制格式。


