两级逻辑实现

在两级逻辑中，输入和输出之间存在的最大级数为 2。这意味着，无论逻辑门的总数是多少，在两级逻辑中，任何输入和输出之间存在(级联)的逻辑门的最大数量为 2。在这里，第一级逻辑门的输出作为第二级逻辑门的输入连接。

考虑四个逻辑门 AND、OR、NAND 和 NOR。由于有 4 个逻辑门，我们将得到 16 种实现两级逻辑的可能方法。这些是AND-AND，AND-OR，ANDNAN​​D，AND-NOR，OR-AND，OR-OR，OR-NAND，OR-NOR，NAND-AND，NAND-OR，NANDNAN​​D，NAND-NOR，NOR-AND，NOR-OR，NOR-NAND，NOR-NOR。

这些两级逻辑实现可以分为以下两类。

• 退化形式
• 非退化形式

退化形式

如果两级逻辑实现的输出可以通过单个逻辑门获得，则称为退化形式。显然，单个逻辑门的输入数量增加。因此，逻辑门的扇入增加。这是退化形式的一个优点。

在 16 种组合中，只有 6 种组合 属于退化形式的两级逻辑实现。它们是 AND-AND、AND-NAND、OR-OR、OR-NOR、NAND-NOR、NORNAND。

在本节中，让我们讨论一些实现。假设 A、B、C 和 D 是每个逻辑实现中的输入，Y 是输出。

AND-AND 逻辑

在此逻辑实现中，AND 门存在于两个级别中。下图显示了 AND-AND 逻辑 实现的示例。

我们将得到第一级逻辑门的输出，因为 Y₁ = AB 和 Y₂ = CD

这些输出 Y₁ 和 Y₂ 用作第二级 AND 门的输入。因此，该 AND 门的输出为

$$\mathrm{Y\:=\:Y_{1}Y_{2}}$$

将 Y₁ 和 Y₂ 值代入上述等式中。

$$\mathrm{Y \: = \: (AB)(CD)}$$

$$\mathrm{\Rightarrow \: Y \: = \: ABCD}$$

因此，该 AND-AND 逻辑实现的输出为 ABCD。该布尔函数可使用 4 输入 AND 门来实现。因此，它是退化形式。

AND-NAND 逻辑

在此逻辑实现中，AND 门存在于第一级，NAND 门存在于第二级。下图显示了 AND-NAND 逻辑 实现的示例。

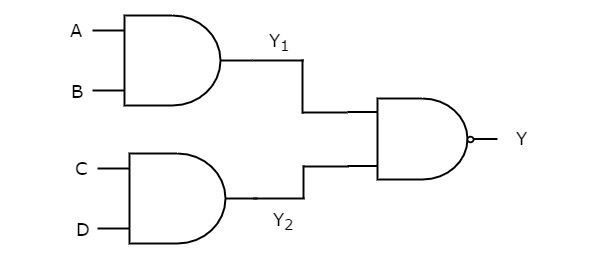
之前，我们得到第一级逻辑门的输出为 Y₁ = AB 和 Y₂ = CD

这些输出 Y₁ 和 Y₂ 用作第二级 NAND 门的输入。因此，此 NAND 门的输出为

$$\mathrm{Y \: = \:(Y_{1}Y_{2})'}$$

将 Y₁ 和 Y₂ 值代入上述等式中。

$$\mathrm{Y \: = \: ((AB)(CD))'}$$

$$\mathrm{\Rightarrow \: Y \: = \: (ABCD)'}$$

因此，此 AND-NAND 逻辑实现的输出为 (ABCD)'。此布尔函数可使用 4 输入 NAND 门来实现。因此，它是退化形式。

OR-OR 逻辑

在此逻辑实现中，OR 门存在于两个级别中。下图显示了 OR-OR 逻辑 实现的示例。

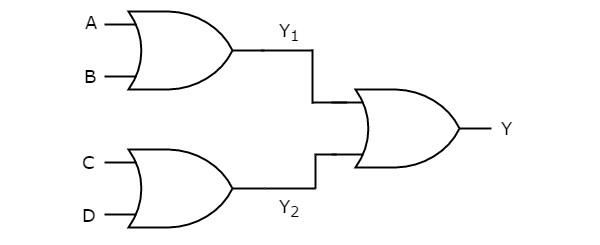
我们将得到第一级逻辑门的输出，即 Y₁ = A + B 和 Y₂ = C + D。

这些输出 Y₁ 和 Y₂ 用作第二级 OR 门的输入。因此，该或门的输出为

$$\mathrm{Y \:= \: Y_{1}\:+\:Y_{2}}$$

在上述等式中代入 Y₁ 和 Y₂ 值。

$$\mathrm{Y \: = \: (A\:+\:B) \: + \: (C\:+\:D)}$$

$$\mathrm{\Rightarrow \: Y \:=\:A\:+\:B\:+\:C\:+\:D}$$

因此，此或-或逻辑实现的输出为A + B + C + D。此布尔函数可使用 4 输入或门来实现。因此，它是退化形式。

同样，您可以验证其余实现是否属于此类别。

非退化形式

如果两级逻辑实现的输出不能通过使用单个逻辑门获得，则称为非退化形式。

两级逻辑实现的其余10 个组合属于非退化形式。这些是 AND-OR、AND-NOR、OR-AND、OR-NAND、NAND-AND、NANDOR、NAND-NAND、NOR-AND、NOR-OR、NOR-NOR。

现在，让我们讨论一些实现。假设 A、B、C 和 D 是输入，Y 是每个逻辑实现中的输出。

AND-OR 逻辑

在此逻辑实现中，AND 门存在于第一级，OR 门存在于第二级。下图显示了 AND-OR 逻辑 实现的示例。

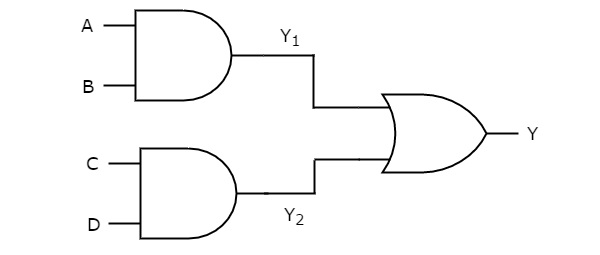
之前，我们得到第一级逻辑门的输出为 Y₁ = AB 和 Y₂ = CD。

这些输出 Y₁ 和 Y₂ 用作第二级 OR 门的输入。因此，该或门的输出为

$$\mathrm{Y\:=\:Y_{1}\:+\:Y_{2}}$$

将 Y₁ 和 Y₂ 值代入上述等式中

$$\mathrm{Y\:=\:AB\:+\:CD}$$

因此，该与或逻辑实现的输出为 AB + CD。该布尔函数为 乘积和 形式。由于我们无法使用单个逻辑门来实现它，因此该与或逻辑实现为 非退化形式。

AND-NOR 逻辑

在此逻辑实现中，AND 门位于第一级，NOR 门位于第二级。下图显示了 AND-NOR 逻辑 实现的示例。

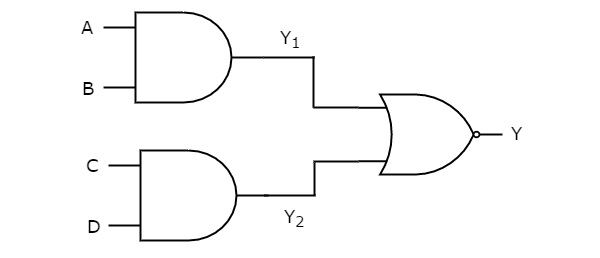
我们知道第一级逻辑门的输出为 Y₁ = AB 和 Y₂ = CD

这些输出 Y₁ 和 Y₂ 用作第二级 NOR 门的输入。因此，该 NOR 门的输出为

$$\mathrm{Y \:=\:(Y_{1}\:+\:Y_{2})'}$$

将 Y₁ 和 Y₂ 值代入上述等式中。

$$\mathrm{Y\:=\:(AB\:+\:CD)'}$$

因此，该 AND-NOR 逻辑实现的输出为 (AB + CD)'。该布尔函数为 AND-OR-Invert 形式。由于我们无法使用单个逻辑门来实现它，因此这种 AND-NOR 逻辑实现是一种非退化形式

OR-AND 逻辑

在此逻辑实现中，OR 门存在于第一级，AND 门存在于第二级。下图显示了 OR-AND 逻辑 实现的一个示例。

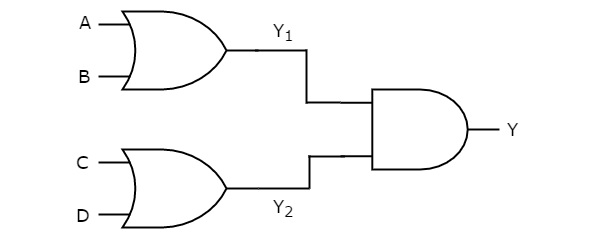
之前，我们得到第一级逻辑门的输出为 Y₁ = A + B 和 Y₂ = C + D。

这些输出 Y₁ 和 Y₂ 用作第二级 AND 门的输入。因此，该与门的输出为

$$\mathrm{Y\:=\:Y_{1}Y_{2}}$$

将 Y₁ 和 Y₂ 值代入上述等式中。

$$\mathrm{Y \: = \: (A\:+\:B)(C\:+\:D)}$$

因此，该或与逻辑实现的输出为 (A + B) (C + D)。该布尔函数为和的乘积形式。由于我们无法使用单个逻辑门来实现它，因此这种"或与"逻辑实现是一种非退化形式。

同样，您可以验证其余实现是否属于此类别。