数字电子中的全加器
什么是全加器?
可以将两个二进制数字(位)和一个进位位相加,并产生一个和位和一个进位位作为输出的组合逻辑电路称为全加器。
换句话说,设计用于将三个二进制数字相加并产生两个输出(和和进位)的组合电路称为全加器。因此,全加器电路将三个二进制数字相加,其中两个是输入,一个是从上一次加法转发的进位。全加器的框图和电路图如图 1 所示。
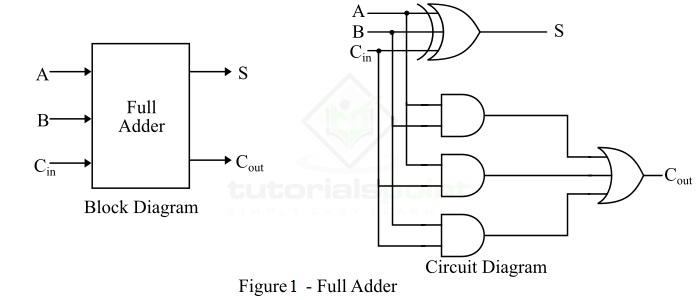
因此,全加器的电路由一个异或门、三个与门和一个或门组成,它们连接在一起,如图 1 中的全加器电路所示。
全加器的操作
全加器有三个输入,即 A、B 和 Cin。其中,A 和 B 是两个二进制数字,Cin 是来自上一级二进制加法的进位位。全加器的总和输出是通过对位 A、B 和 Cin 进行异或运算获得的。而进位输出位(Cout)则通过AND和OR运算获得。
全加器的真值表
真值表表示逻辑电路输入和输出变量之间的关系,并解释逻辑电路的操作。以下是全加器电路的真值表 −
| 输入 | 输出 | |||
|---|---|---|---|---|
| A | B | Cin | S (Sum) | Cout (Carry) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
因此,从真值表可以清楚地看出,当只有 1 个输入等于 1 或所有输入都等于 1 时,全加器的和输出等于 1。而当两个或三个输入等于 1 时,进位输出的进位为 1。
全加器的 K-Map
K-Map(卡诺图)是一种简化二进制复杂布尔代数表达式的工具。全加器的 K-Map 如图 2 所示。
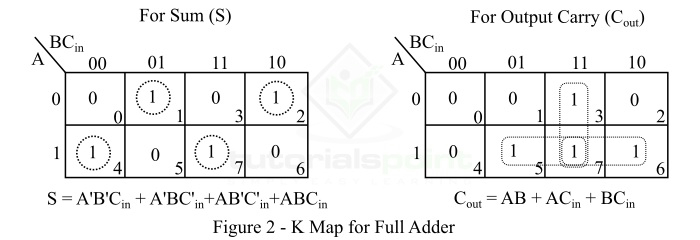
全加器的特征方程
全加器的特征方程,即和 (S) 和进位输出 (Cout) 的方程是根据二进制加法规则得出的。这些方程如下所示 −
全加器的和 (S) 是 A、B 和 Cin 的异或。因此,
$$\mathrm{Sum, \: S \: = \: A \: \oplus \: B \: \oplus \: C_{in} \: = \: A'B'C_{in} \: + \: A'BC'_{in} \: + \: AB'C'_{in} \: + \: ABC_{in} }$$
半加器的进位 (C) 是 A 与 B 的 AND。因此,
$$\mathrm{Carry, \: C \: = \: AB \: + \: AC_{in} \: + \: BC_{in}}$$
全加器的优点
以下是全加器相对于半加器的重要优点 −
- 全加器提供了从前一阶段添加进位的功能。
- 与半加器相比,全加器消耗的功率相对较小。
- 只需在电路中添加一个非门,即可轻松将全加器转换为半减法器。
- 全加器比半加器产生更高的输出。
- 全加器是多路复用器等关键数字电路的重要组成部分之一。
- 全加器以更高的速度执行操作。
全加器的应用
以下是全加器的重要应用−
- 全加器用于计算机 CPU 的 ALU(算术逻辑单元)。
- 全加器用于计算器。
- 全加器还有助于执行二进制数的乘法。
- 全加器还用于实现关键数字电路,如多路复用器。
- 全加器用于生成内存地址。
- 全加器还用于生成程序计数器。
- 全加器还用于 GPU(图形处理单元)。
结论
在本教程中,我们讨论了与数字电子中的全加器相关的所有关键概念。全加器在许多数字电子电路中起着重要作用,因为全加器可用于实现其他几个关键数字电路。


