数字电子技术 - 编码器
编码器是一种组合逻辑电路,用于将正常或熟悉的信息转换为编码格式。换句话说,编码器是一种数字设备,它将以十进制数字和字母字符形式表示的信息转换为二进制表示形式的编码形式。编码器执行的操作称为编码。
在本章中,我们将解释编码器的基础知识和常用的编码器类型。
什么是编码器?
编码器是一种数字组合电路,它将人性化的信息转换为编码格式,以便使用机器进行处理。简而言之,编码器将信息从正常形式转换为编码形式。这个过程称为编码。
编码器是各种数字电子应用(如数据传输、控制和自动化、通信、信号处理等)中的关键组件。
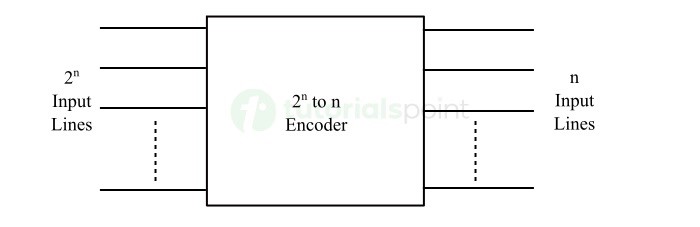
编码器由一定数量的输入和输出线组成。其中,编码器最多可以有"2n"条输入线,而"n"条输出线。因此,编码器用"n"位对"2n"条输入线表示的信息进行编码。
编码器的框图如下图所示 −
现在让我们讨论一下数字电子应用中常用的不同类型的编码器。
编码器的类型
数字电子中一些常用的编码器类型 −
- 4 到 2 编码器
- 8 到 3 编码器(八进制编码器)
- 十进制到 BCD 编码器
现在让我们讨论一下数字电子中最常用的三种编码器详细信息。
4 对 2 编码器
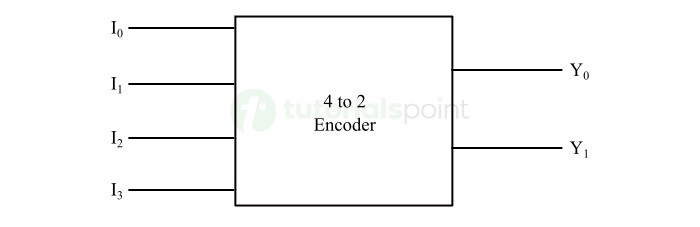
4 对 2 编码器是一种具有 4 (22) 条输入线和 2 条输出线的编码器。它根据输入线的组合产生输出代码(即以 2 位格式转换输入信息)。
下图显示了 4 对 2 编码器的框图。
以下真值表 − 描述了 4 对 2 编码器针对不同输入组合的工作原理
| 输入 | 输出 | ||||
|---|---|---|---|---|---|
| I3 | I2 | I1 | I0 | Y1 | Y0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
从该真值表中,我们可以得出 4 对 2 编码器每个输出的布尔表达式如下 −
$$\mathrm{Y_{0} \: = \: I_{1} \: + \: I_{3}}$$
$$\mathrm{Y_{1} \: = \: I_{2} \: + \: I_{3}}$$
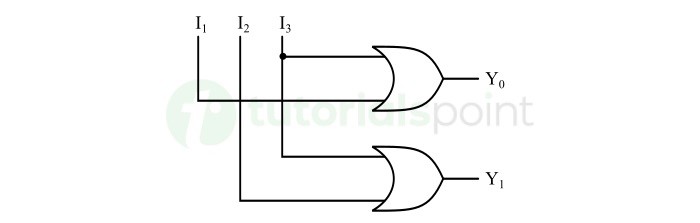
很明显,我们可以使用两个或门来实现 4 对 2 编码器的逻辑电路。下图描述了 4 对 2 编码器的逻辑图。
4 对 2 编码器的应用
4 对 2 编码器广泛应用于以下应用:数据复用、生成数字控制信号、地址解码应用、在数字系统中编码数据等。
八进制到二进制编码器
八进制到二进制编码器是一种将八进制代码转换为二进制代码的编码器。它接受 8 条输入线,并根据输入线的组合产生 3 位输出。因此,它也被称为8 到 3 编码器。
下图显示了八进制到二进制编码器的框图 −
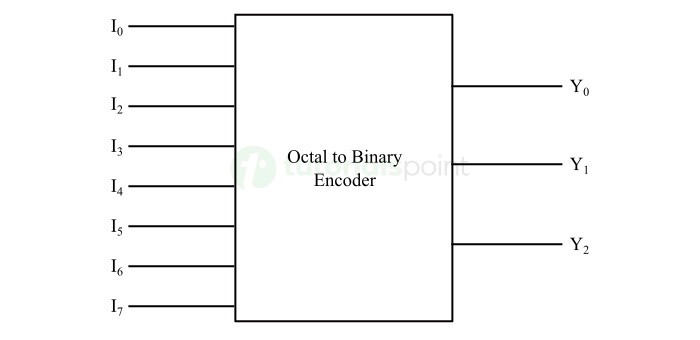
以下真值表描述了八进制到二进制编码器的工作原理 −
| 输入 | 输出 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| I7 | I6 | I5 | I4 | I3 | I2 | I1 | I0 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
从这个真值表中,我们可以写出八进制到二进制编码器输出的布尔表达式,如下所示。
$$\mathrm{Y_{0} \: = \: I_{1} \: + \: I_{3} \: + \: I_{5} \: + \: I_{7}}$$
$$\mathrm{Y_{1} \: = \: I_{2} \: + \: I_{3} \: + \: I_{6} \: + \: I_{7}}$$
$$\mathrm{Y_{2} \: = \: I_{4} \: + \: I_{5} \: + \: I_{6} \: + \: I_{7}}$$
从这些表达式中可以清楚地看出,八进制到二进制编码器的实现需要 3 个或门。
八进制转二进制编码器的逻辑电路图如下图所示 −
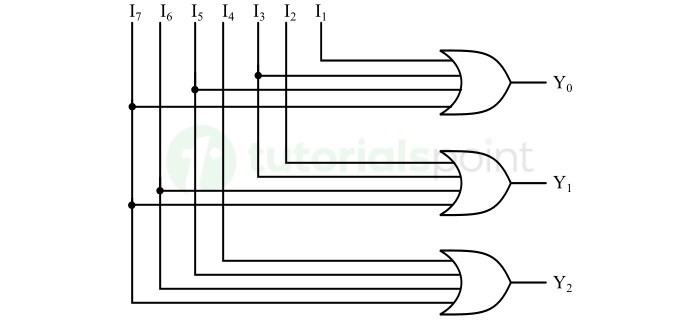
八进制转二进制编码器的应用
八进制转二进制编码器用于以下应用 −
- 数字系统中的数据转换。
- 将八进制内存地址转换为二进制内存地址。
- 在微处理器和微控制器中,将八进制指令转换为二进制格式。
- 在通信系统中,将八进制数据编码为二进制形式进行传输等。
十进制转 BCD 编码器
一种可以将十进制转换为二进制的编码器。将十进制数或用十进制数表示的信息转换为其等效的二进制编码十进制 (BCD) 格式的过程称为十进制到 BCD 编码器。
在 BCD 编码方案中,每个十进制数字都可以转换为 4 位二进制表示。下表显示了从 0 到 9 的十进制数字的 BCD 等效值。
| 十进制数字 | BCD 代码 | |||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
十进制转 BCD 编码器接受 10 条输入线,并根据输入线的组合产生 4 位 BCD 输出。因此,有时也称为 10 转 4 编码器。
下图为十进制转 BCD 编码器的框图。
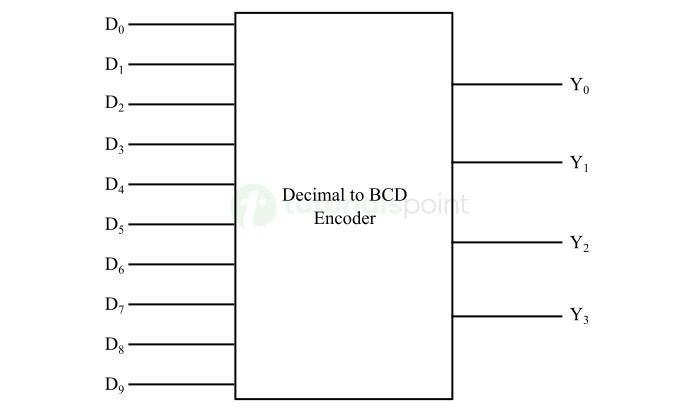
下面给出了描述十进制转 BCD 编码器工作原理的真值表 −
| 输入 | 输出 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D9 | D8 | D7 | D6 | D5 | D4 | D3 | D2 | D1 | D0 | Y3 | Y2 | Y1 | Y0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
从这个真值表,我们可以写出十进制到BCD编码器的布尔表达式如下。
$$\mathrm{Y_{0} \: = \: D_{1} \: + \: D_{3} \: + \: D_{5} \: + \: D_{7} \: + \: D_{9}}$$
$$\mathrm{Y_{1} \: = \: D_{2} \: + \: D_{3} \: + \: D_{6} \: + \: D_{7}}$$
$$\mathrm{Y_{2} \: = \: D_{4} \: + \: D_{5} \: + \: D_{6} \: + \: D_{7}}$$
$$\mathrm{Y_{3} \: = \: D_{8} \: + \: D_{9}}$$
可以使用四个或门来实现十进制到 BCD 编码器的逻辑电路,如下图所示 −

十进制到 BCD 编码器的应用
十进制到BCD 编码器可用于数字时钟和计时器、数据处理设备和存储系统、计算器、测量仪器、显示设备、微处理器、微控制器、嵌入式系统等。
结论
编码器将信息转换为特定的编码格式。编码器是各种数字系统中必不可少的元素,例如自动化和控制系统、通信系统和存储单元、计算和计算设备、测量仪器、数据转换器等。
在本章中,我们介绍了最广泛使用的编码器类型,它们是 4 到 2 编码器、八进制到二进制编码器和十进制到 BCD 编码器。


