通过 NAND 门实现 XOR 门
NAND 门是一种通用逻辑门,使用它我们可以实现任何其他类型的逻辑门或逻辑表达式。阅读本教程以了解如何仅使用 NAND 门实现 XOR 门。让我们从 XOR 和 NAND 门的基本概述开始
什么是 XOR 门?
XOR(异或)门是一种派生逻辑门。XOR 门是一种具有两个输入和一个输出的逻辑门。当 XOR 门的两个输入中有且只有一个为高电平(逻辑 1)时,XOR 门会产生高电平(逻辑 1)输出。当 XOR 门的两个输入均为高电平(逻辑 1)或低电平(逻辑 0)时,XOR 门的输出为低电平(逻辑 0)状态。 XOR 门 a 的逻辑符号如图 1 所示。

因此,仅当 XOR 门的输入不相等时,其才会产生高电平输出。因此,异或门又被称为"反符合门"或"不等式检测器"。
异或门的输出方程
异或门的输出是其输入的模和,即
$$\mathrm{Y \: = \: A \oplus B \: = \: A \: \bar{B} \: + \: \bar{A} \: B}$$
其中,A和B是异或门的两个输入变量,Y是异或门的输出变量。 XOR 门的输出表达式为 Y 等于 A 异或 B。
XOR 门的真值表
真值表显示了 XOR 门的输入和输出之间的关系。XOR 门的真值表如下所示。
| 输入 | 输出 | |
|---|---|---|
| A | B | Y = (AB' + A'B) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
什么是 NAND 门?
NAND 门是一种通用逻辑门,可用于实现任何类型的逻辑表达式或任何其他类型的逻辑门。NAND 门基本上是两个基本逻辑门的组合,即 AND 门和非门,即
$$\mathrm{NAND \: Logic \: = \: AND \: Logic \: = \: NOT \: Logic}$$
NAND 门是一种逻辑门,当其所有输入都为高电平时,其输出为低电平(逻辑 0),当其任何输入为低电平(逻辑 0)时,其输出为高电平(逻辑 1)。因此,NAND 门的操作与 AND 门的操作相反。图 2 显示了双输入 NAND 门的逻辑符号。

NAND 门的输出方程
如果 A 和 B 是输入变量,Y 是 NAND 门的输出变量,则其输出由以下公式给出
$$\mathrm{Y \: = \: \overline{A \cdot B} \: = \: (A \cdot B)'}$$
读作"Y 等于 A·B 整条"。
NAND 真值表门
以下是 NAND 门的真值表 −
| 输入 | 输出 | |
|---|---|---|
| A | B | Y = (A.B)' |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
现在,让我们讨论如何从 NAND 门实现 XOR 门。
从 NAND 门实现 XOR 门
如上所述,NAND 门是一种通用逻辑,因此,我们可以使用它来实现任何其他逻辑门。图 3 显示了如何仅使用 NAND 门实现 XOR 门。
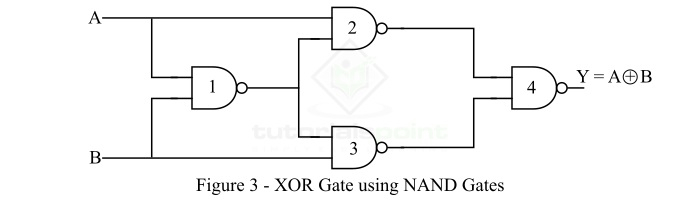
从仅使用 NAND 门的 XOR 门的逻辑电路图中可以看出,我们需要 4 个 NAND 门。
现在,让我们了解这个 NAND 逻辑电路如何产生与 XOR 门等效的输出。
第一个 NAND 门的输出是,
$$\mathrm{Y_{1} \: = \: \overline{A \: B}}$$
第二和第三个 NAND 门的输出是,
$$\mathrm{Y_{2} \: = \: \overline{A \cdot \overline{AB}}}$$
$$\mathrm{Y_{3} \: = \: \overline{B \cdot \overline{AB}}}$$
最后,这两个输出(Y2 和 Y3)连接到第四个 NAND 门。这个 NAND 门将产生一个输出,
$$\mathrm{Y \: = \: \overline{\overline{A \cdot \overline{AB}} \cdot \overline{B \cdot \overline{AB}}}}$$
$$\mathrm{\Rightarrow \: Y \: = \: A \cdot \overline{AB} \: + \: B \cdot \overline{AB} \: = \: A(\bar{A} \: + \: \bar{B}) \: + \: B(\bar{A} \: + \: \bar{B})}$$
$$\mathrm{\Rightarrow \: Y \: = \: A \: \bar{A} \: + \: A \: \bar{B} \: + \: \bar{A} \: B \: + \: B \: \bar{B}}$$
$$\mathrm{\therefore \: Y \: = \: A \: \bar{B} \: + \: \bar{A} \: B \: = \: A \oplus B}$$
这是 XOR 门的输出。因此,通过这种方式,我们可以仅从 NAND 门实现 XOR 门。


