移位寄存器的应用
在上一章中,我们讨论了四种类型的移位寄存器。根据需求,我们可以使用其中一种移位寄存器。以下是移位寄存器的应用。
移位寄存器用作并行到串行转换器,将并行数据转换为串行数据。它用于模拟到数字转换器 (ADC) 块之后的发射器部分。
移位寄存器用作串行到并行转换器,将串行数据转换为并行数据。它用于数字到模拟转换器 (DAC) 块之前的接收器部分。
移位寄存器与一些附加门一起生成零和一的序列。因此,它用作序列生成器。
移位寄存器也用作计数器。根据最右边 D 触发器连接到串行输入的输出类型,有两种类型的计数器。它们是环形计数器和约翰逊环形计数器。
在本章中,我们将逐一讨论这两个计数器。
环形计数器
在上一章中,我们讨论了串行输入 - 并行输出(SIPO)移位寄存器的操作。它以串行形式从外部接受数据,并且需要"N"个时钟脉冲才能移位"N"位数据。
类似地,"N"位环形计数器执行类似的操作。但是,唯一的区别是,最右边 D 触发器的输出作为最左边 D 触发器的输入,而不是从外部应用数据。因此,环形计数器产生一系列状态(零和一的模式),并且每'N'个时钟周期重复一次。
下图显示了3位环形计数器的框图。
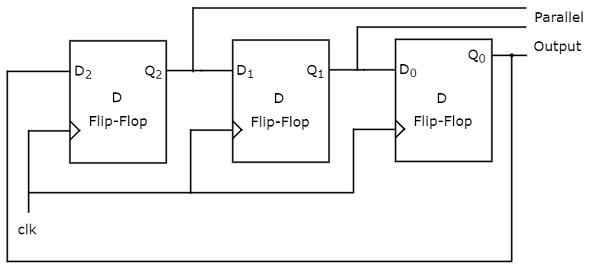
3位环形计数器仅包含一个3位SIPO移位寄存器。最右边的D触发器的输出连接到最左边的D触发器的串行输入。
假设从最左边到最右边的D触发器的初始状态为$\mathrm{Q_{2}Q_{1}Q_{0} \: = \: 001}$。这里,$\mathrm{Q_{2}}$ & $\mathrm{Q_{0}}$ 分别为 MSB 和 LSB。我们可以从下表中了解环形计数器的工作原理。
| 时钟上升沿数 | 串行输入 = Q0 | Q2(MSB) | Q1 | Q0(LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 0 | 1 |
在没有时钟信号的情况下,D 触发器的初始状态为 $\mathrm{Q_{2}Q_{1}Q_{0} \: = \: 001}$。此状态在时钟信号的每三个正沿转换时重复一次。
因此,以下操作在时钟信号的每个正沿发生。
第一个 D 触发器的串行输入获取第三个触发器的先前输出。因此,第一个 D 触发器的当前输出等于第三个触发器的先前输出。
第一和第二个 D 触发器的先前输出右移一位。这意味着,第二和第三个 D 触发器的当前输出等于第一和第二个 D 触发器的先前输出。
约翰逊环形计数器
约翰逊环形计数器的操作与环形计数器的操作类似。但是,唯一的区别是,最右边 D 触发器的补码输出作为最左边 D 触发器的输入,而不是正常输出。因此,"N"位约翰逊环形计数器产生一系列状态(零和一的模式),并且每"2N"个时钟周期重复一次。
约翰逊环形计数器也称为扭曲环形计数器和开关尾环形计数器。下图显示了 3 位约翰逊环形计数器的框图。
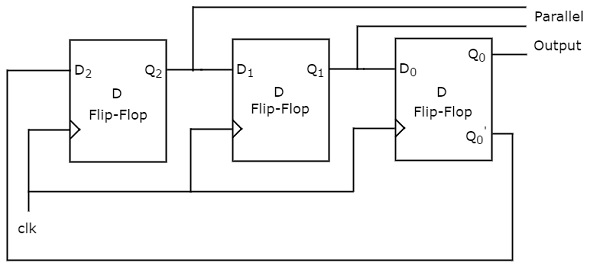
3 位约翰逊环形计数器也仅包含一个 3 位 SIPO 移位寄存器。最右侧 D 触发器的补码输出连接到最左侧 D 触发器的串行输入。
假设最初所有 D 触发器都已清除。因此,$\mathrm{Q_{2}Q_{1}Q_{0} \: = \: 000}$。这里,$\mathrm{Q_{2}}$ & $\mathrm{Q_{0}}$ 分别为 MSB 和 LSB。我们可以从下表中了解约翰逊环形计数器的工作原理。
| 时钟上升沿数 | 串行输入 = Q0 | Q2(MSB) | Q1 | Q0(LSB) |
|---|---|---|---|---|
| 0 | - | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 2 | 1 | 1 | 1 | 0 |
| 3 | 1 | 1 | 1 | 1 |
| 4 | 0 | 0 | 1 | 1 |
| 5 | 0 | 0 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 |
在没有时钟信号的情况下,D 触发器的初始状态为 $\mathrm{Q_{2}Q_{1}Q_{0} \: = \: 000}$。此状态在时钟信号的每六个正沿转换时重复一次。
因此,以下操作在时钟信号的每个正沿发生。
第一个 D 触发器的串行输入获得第三个触发器的先前补码输出。因此,第一个 D 触发器的当前输出等于第三个触发器的先前补码输出。
第一和第二个 D 触发器的先前输出右移一位。这意味着,第二和第三个 D 触发器的当前输出等于第一和第二个 D 触发器的先前输出。


