数字电子技术 - 阈值逻辑
在前面的章节中,我们已经使用逻辑门实现了各种组合电路。除了非门之外,其余所有逻辑门都至少有两个输入和一个输出。类似地,阈值门也包含至少一个输入和只有一个输出。
此外,它还包含每个输入的相应权重和一个阈值。这些权重和阈值的值可以是任何有限实数。
阈值门基础知识
假设阈值门的输入为 X1、X2、X3、…、Xn。这些输入的相应权重为 W1、W2、W3、…、Wn。阈值门的符号如下图所示。
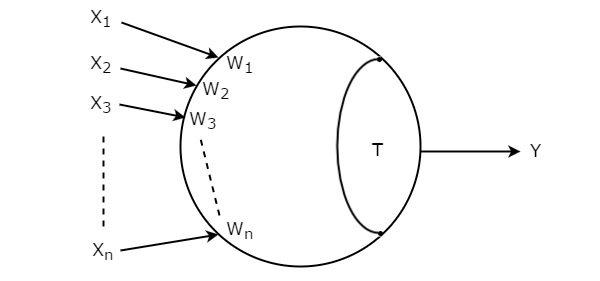
阈值门用圆圈表示,有"n"个输入,X1到Xn和单个输出Y。这个圆圈分为两部分。一部分表示与输入相对应的权重,另一部分表示阈值T。
输入与相应权重的乘积之和称为加权和。如果这个加权和大于或等于阈值T,那么只有输出Y等于一。否则,输出 Y 将等于零。
从数学上讲,我们可以将阈值门的输入和输出之间的关系写如下。
$$\mathrm{Y \: = \: 1 \:\: if \: \: W_{1}X_{1} \: + \: W_{2}X_{2} \: + \: W_{3}X_{3} \: + \: \dotso \: + \: W_{n}X_{n} \: \geq \: T}$$
𝑌 = 0,否则。
因此,我们可以实现各种逻辑门和布尔函数只需改变权重和/或阈值 T 的值即可。
示例
让我们为以下阈值门找到简化的布尔函数。
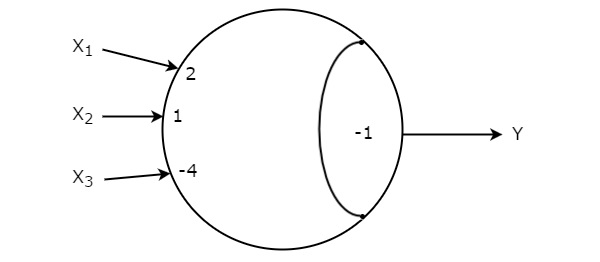
此阈值门具有三个输入 X1、X2、X3 和一个输出 Y。
与输入 X1、X2 和 X3 对应的权重为 W1 = 2、W2 = 1 和W3 = -4。
阈值门的值为T = -1。
阈值门的加权和为
$$\mathrm{W \: = \: W_{1}X_{1} \: + \: W_{2}X_{2} \: + \: W_{3}X_{3}}$$
将给定的权重代入上述等式。
$$\mathrm{\Rightarrow \: W \: = \: 2X_{1} \: + \: X_{2} \: − \: 4X_{3}}$$
阈值门的输出,如果 W ≥ −1,则 Y 将为 '1',否则将为 '0'。
以下表格显示了所有可能的输入组合的输入和输出之间的关系。
| 输入 | 加权和 | 输出 | ||
|---|---|---|---|---|
| X1 | X2 | X3 | W = 2X1 + X2 - 4X3 | Y |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | -4 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | -3 | 0 |
| 1 | 0 | 0 | 2 | 1 |
| 1 | 0 | 1 | -2 | 0 |
| 1 | 1 | 0 | 3 | 1 |
| 1 | 1 | 1 | -1 | 1 |
从上表中,我们可以将输出 Y 的布尔函数写为
$$\mathrm{Y \: = \: \sum m( 0,2,4,6,7)}$$
使用3 变量 K-Map简化此布尔函数如下图所示。
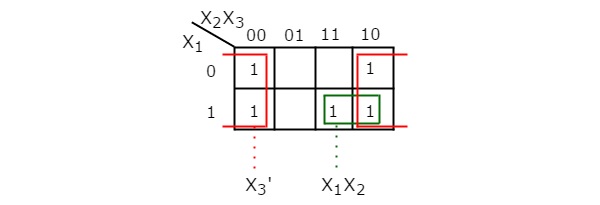
因此,给定阈值门的简化布尔函数为 Y = X3' + X1 X2。
阈值函数的合成
阈值门为也称为通用门,因为我们可以使用阈值门实现任何布尔函数。有时,可能无法使用单个阈值门实现几个逻辑门和布尔函数。在这种情况下,我们可能需要多个阈值门。
按照这些步骤使用单个阈值门实现布尔函数。
步骤 1 − 为给定的布尔函数制定真值表。
步骤 2 − 在上面的真值表中,添加(包括)一列,给出加权总和和阈值之间的关系。
步骤 3 −写出下面提到的每个输入组合的加权和与阈值之间的关系。
- 如果布尔函数的输出为 1,则加权和将大于或等于这些输入组合的阈值。
- 如果布尔函数的输出为 0,则加权和将小于这些输入组合的阈值。
步骤 4 − 选择权重和阈值的值,使它们满足上表最后一列中的所有关系。
步骤 5 −用这些权重和阈值绘制阈值门的符号。
示例
让我们使用单个阈值门实现以下布尔函数。
$$\mathrm{Y( X_{1},X_{2},X_{3})\:=\: \sum m ( 0,2,4,6,7)}$$
给定的布尔函数是一个三变量函数,以最小项和形式表示。此函数的真值表如下所示。
| 输入 | 输出 | ||
|---|---|---|---|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
现在,让我们在上面的真值表中添加(包括)一列。最后一列包含每个输入组合的加权和(W)与阈值值(T)之间的关系。
| 输入 | 输出 | W 与 T 之间的关系 | ||
|---|---|---|---|---|
| X1 | X2 | X3 | Y | |
| 0 | 0 | 0 | 1 | $\mathrm{0 \: \geq \: T}$ |
| 0 | 0 | 1 | 0 | $\mathrm{W_{3} \: \lt \: T}$ |
| 0 | 1 | 0 | 1 | $\mathrm{W_{2} \: \geq \: T}$ |
| 0 | 1 | 1 | 0 | $\mathrm{W_{2}+W_{3} \: \lt \: T}$ |
| 1 | 0 | 0 | 1 | $\mathrm{W_{1} \: \geq \: T}$ |
| 1 | 0 | 1 | 0 | $\mathrm{W_{1}+W_{3} \: \lt \: T}$ |
| 1 | 1 | 0 | 1 | $\mathrm{W_{1}+W_{2} \: \geq \: T}$ |
| 1 | 1 | 1 | 1 | $\mathrm{W_{1}+W_{2}+W_{3} \: \geq \: T}$ |
以下是从上表得出的结论。
- 根据第一个关系,Threshold 的值应为零或负数。
- 根据第一和第二个关系,W3 的值应为负数。
- 根据第五个和第三个关系,W1 和 W2 的值应大于或等于 Threshold 值。
- 根据第四个关系,W2 应大于 W3。
根据上述结论,我们可以为权重和 Threshold 选择以下值。
W1 = 2, W2 = 1, W3 = -4 & T = -1
具有上述值的阈值门的符号如下所示。
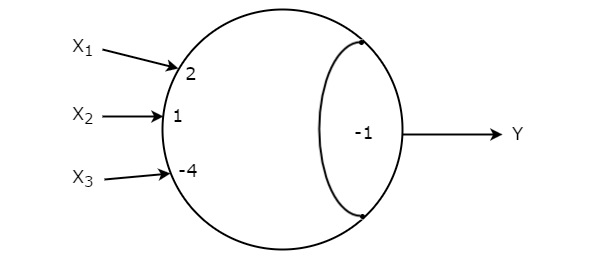
因此,此阈值门实现了给定的布尔函数,$\mathrm{Y( X_{1}, X_{2},X_{3}) \:=\: \sum m (0,2,4,6,7)}$。


