并行加法器和并行减法器
在数字电子技术中,加法器和减法器是两种最基本的算术组合电路。加法器是一种组合算术电路,用于执行两个或多个二进制数的加法。而减法器是一种组合算术电路,用于执行两个二进制数的减法。
根据执行二进制数加法和减法的形式,加法器和减法器分为以下类型 −
- 串行加法器
- 并行加法器
- 串行减法器
- 并行减法器
本教程旨在解释并行加法器和并行减法器。但在此之前,让我们先讨论一下执行二进制加法和减法时遵循的布尔代数规则。
二进制加法
执行二进制加法时遵循以下规则 −
| 二进制数字 A | 二进制数字 B | 和 (A + B) | 进位 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
二进制减法
执行二进制减法时应遵循以下规则 −
| 二进制数字 A | 二进制数字 B | 差 (A - B) | 借位 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
现在,让我们详细讨论并行加法器和并行减法器。
什么是并行加法器?
将两个任意位长的二进制数以并行形式相加并以并行形式产生这两个数之和的数字电路称为并行加法器。
并行加法器基本上由链式全加器组成,如图 1 所示。这里,每个全加器的输出位连接到链中下一个全加器电路的输入进位端。

图 1 所示的并行加法器是一个 4 位并行加法器,因为它可以添加两个 4 位二进制数。但是,我们可以通过增加链中全加器的数量来设计任意位数的并行加法器电路。
在上述并行加法器电路中,位 A 表示被加数位,位 B 表示加数位。并行加法器的第一个输入进位位是 Cin,并行加法器的输出进位位是 C4。输出和位由 S 指定。我们还可以以 IC 的形式构建并行加法器。例如,当 4 位并行加法器以 IC 形式形成时,它将具有 4 个端子用于加数位,4 个端子用于加数位,4 个端子用于和位,以及 2 个端子用于输入和输出进位位。
并行加法器的工作原理
图 1 所示的并行加法器按照以下步骤执行两个数字的二进制加法 −
步骤 1 − 首先,全加器电路 FA1 将位 A1 和 B1 与输入进位位 Cin 相加以产生和位 S1,其中它是输出和的 LSB(最低有效位)。在此阶段,生成进位位 C1,该位被传输到链中的下一个全加器电路。
步骤 2 − 全加器电路 FA2 将位 A2 和 B2 以及来自前一次加法的进位位 C1 相加。它生成和位 S2,即输出和的第二位,并且还生成进位位 C2,该位再次转发到下一个全加器 FA3。
步骤 3 −全加器电路 FA3 将输入位 A3 和 B3 以及来自前一次加法的进位位 C2 相加,以产生和位 S3 和进位位 C3。
步骤 4 − 全加器 FA4 将输入位 A4 和 B4 以及来自 FA3 的进位位 C3 相加。它生成最后一个和位 S4 和最后一个进位位 C4。
步骤 5 −然后,并行加法器的输出和由以下公式给出:
$$\mathrm{S_{out} \: = \: C_{4} \: S_{4} \: S_{3} \: S_{2} \: S_{1}}$$
什么是并行减法器?
用于求两个二进制数并行算术差的数字算术电路称为并行减法器。
我们可以通过多种方式实现并行减法器,例如组合半减法器和全减法器、全全减法器、全全加法器等。在这里,我们实现了一个 4 位并行减法器,使用全加法器,减数位补码,如图 2 所示。
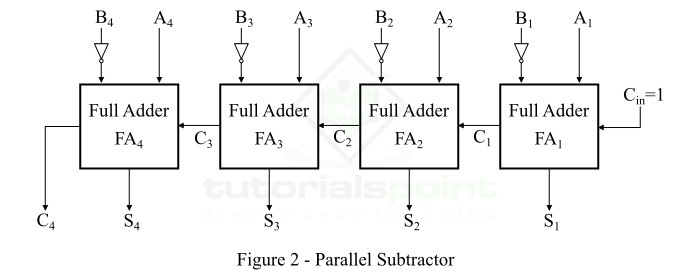
这是 4 位并行减法器,但是,我们可以通过在图 2 所示的电路链中添加任意数量的全加器来实现并行减法器。
两个二进制数的二进制减法可以方便地通过 1 或 2 的补码来实现。其中,补码方法将减法运算转换为简单的加法运算。
二进制数的 2 的补码是通过取 1 的补码并将 1 加到最低有效位对上获得的。1 的补码可以借助非门(反相器)来实现。
并行减法器的工作原理
上图 2 所示的并行减法器按照以下步骤对两个二进制数进行减法 −
步骤 1 − 首先,将使用反相器获得的位 B1 的 1 的补码与 1(Cin)相加,以获得位 B1 的 2 的补码。然后,将此 2 的补码 B1 进一步添加到 A1。这将产生由 S1 指定的输出差的第一位,以及与 FA2 的输入进位相连的进位位 C1。
步骤 2 −全加器 FA2 使用输入进位位 C1 与其输入位 A2 以及输入位 B2 的 2 的补码相加,得到第二个差值位 (S2) 和进位位 C2。
步骤 3 − 全加器 FA3 使用输入进位位 C2 与其输入位 A3 以及输入位 B3 的 2 的补码相加,得到第三个差值位 (S3) 和进位位 C3。
步骤 4 −最后,全加器 FA4 使用进位位 C3 与其输入位 A4 和输入位 B4 的 2 的补码相加,以产生最后一个差位 (S4) 和最后一个进位位 C4。
一旦产生所有结果位,它们将被表示为两个二进制数的差,即 S4S3S2S1 和借位位 C4。
结论
这就是数字电子技术中关于并行加法器和并行减法器的全部内容。并行加法器和减法器最显著的优势是,与串行加法器和减法器相比,它们可以更快地执行两个二进制数的算术加法和减法。


