布尔表达式的最大项表示

K-Map或卡诺图是一种简化复杂布尔函数或表达式的系统方法。K-Map 基本上是一个由一定数量的相邻单元格组成的图形或图表。每个单元格以和或乘积形式表示变量的特定组合。

但是，我们可以使用 K-Map 来简化任意数量变量的布尔函数，但对于涉及五个或更多变量的函数，它会变得繁琐。在实际操作中，我们通常使用 K-Map 来简化最多六个变量的布尔函数。

n 个变量的布尔函数在乘积和 (SOP) 形式中可以有 2ⁿ 种可能的乘积项组合，在和的乘积 (POS) 形式中可以有 2ⁿ 种可能的和项组合。

因此，对于 2 个变量的布尔函数，K-map 将有 2² = 4 个单元格，对于 3 个变量的函数，它将有 2³ = 8 个单元格，依此类推。

布尔函数可以用两种规范或标准形式表示，即 SSOP(标准乘积和)形式和 SPOS(标准和乘积)形式。

SSOP 形式是布尔函数表示为乘积项的和，其中表达式的每个项以补码或非补码形式包含函数的所有变量。 SSOP 形式的逻辑表达式的每个乘积项称为 最小项。

例如，

$$\mathrm{Y \: = \: AB \: + \: \overline{A}B}$$

这里，Y 是两个变量 A 和 B 的布尔函数。项 AB 和 AB' 是函数的最小项。

在 SPOS 形式中，布尔函数表示为和项的乘积，其中每个和项称为 最大项，以补码或非补码形式包含函数的所有变量。

例如，

$$\mathrm{Y \: = \: \lgroup A \: + \: B\rgroup \: .\: \lgroup \overline{A} \: + \: B \rgroup}$$

这里，Y 是两个变量 A 和 B 的布尔函数，项 (A+B) 和 (A'+B) 是该函数的两个最大项。

本文主要是为了解释如何在 K 图上以最大项形式表示布尔函数。因此，让我们讨论一下最大项表示或在 K 图上绘制零点。

绘制零点(最大项表示)

正如我们已经讨论过的，标准 POS 形式表达式中的每个和项都称为最大项。最大项用大写字母 M 表示，下标表示该最大项的十进制名称。

为了将标准 POS 表达式表示到 K 图上，在表达式中表示的最大项对应的单元格中绘制零，在表达式中不存在的最大项对应的单元格中不输入任何内容。

现在，为了更好地理解绘制零或最大项表示的概念，让我们讨论一些已解决的示例。

示例 1

在 K 图上绘制以下 2 变量布尔表达式。

$$\mathrm{Y \: = \: \lgroup A \: + \: B \rgroup\lgroup A \: + \: \overline{B} \rgroup\lgroup \overline{A} \:+ \: B \rgroup}$$

解决方案

给定的布尔表达式的最大项可以表示为，

$$\mathrm{Y \: = \: M_{3} \cdot M_{2} \cdot M_{1} \: = \: \prod M \lgroup 0, \: 1, \: 2 \rgroup}$$

该函数在 K 图上的最大值表示如图 1 所示。

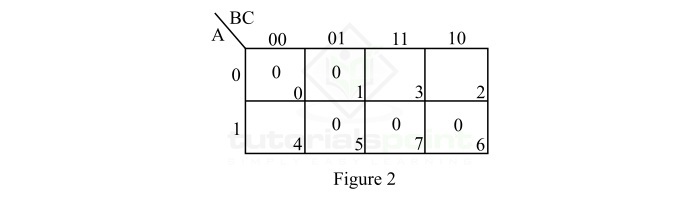
示例 2

在 K 图上绘制以下 3 个变量布尔函数。

$$\mathrm{Y \: = \: \lgroup A \: + \: B \: + \: C \rgroup\lgroup \overline{A} \: + \: \overline{B} \: + \: C\rgroup\lgroup A \: + \: B \: + \: \overline{C}\rgroup\lgroup \overline{A} \: + \: B \: + \: \overline{C} \rgroup\lgroup \overline{A} \: + \: \overline{B} \: + \: \overline{C}\rgroup}$$

解决方案

给定的布尔函数以最大项的形式可以表示为，

$$\mathrm{Y \: = \: M_{0} \cdot M_{1}\cdot M_{5} \cdot M_{6} \cdot M_{7} \: = \: \prod M \lgroup 0, \: 1, \: 5, \: 6, \: 7 \rgroup}$$

该函数在 K 图上的最大值表示如图 2 所示。

因此，这都是关于在 K 图上绘制布尔表达式的零点或最大值表示。

教程问题

尝试解决以下教程问题以更清楚地理解概念。

Q1. 在 K 图上以最大值表示绘制以下布尔表达式K-map。

$$\mathrm{f( A, \: B) \: = \: (A \: + \: B)\cdot(\overline{A} \: + \: B).(\overline{A} \: + \: \overline{B})}$$

Q2. 在 K 图上以最大项表示绘制以下 3 变量布尔函数。

$$\mathrm{f(A, \: B, \: C) \: = \: (A \: + \: B \: + \: \overline{C})\cdot(A \: + \: \overline{B} \: + \: C)\cdot( \overline{A} \: + \: \overline{B} \: + \: C)\cdot(\overline{A} \: + \: B \: + \: \overline{C})}$$