数字电子技术中的与门
在数字电子技术中,有几种不同类型的逻辑门,例如与门、或门、非门等。在本章中,我们将解释与门的理论。
与门是用于实现各种复杂数字电路和系统的基本逻辑门。与门对施加到其上的输入进行逻辑乘法并相应地产生输出。
什么是与门?
与门是用于各种数字电路和系统的一种基本逻辑门。仅当其所有输入均为高电平或逻辑 1 或真时,它才会产生高电平或逻辑 1 或真输出。对于所有其他输入组合,它会产生低或逻辑 0 或 False 输出。
下图描绘了两个和三个输入 AND 门的逻辑符号。
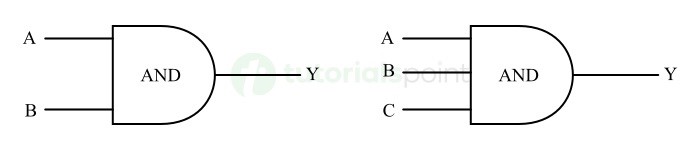
这里,A、B 和 C 是输入变量,Y 是输出变量。
在本章中,我们将介绍只有三个输入的 AND 门。但是我们可以为任意数量的输入变量设计一个与门。
与门的真值表
与门的真值表包含输入和输出,并指定它们之间的关系。
双输入与门的真值表如下所示 −
| 输入 | 输出 | |
|---|---|---|
| A | B | Y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
从这个双输入与门的真值表中可以看出,只有当两个输入均为逻辑 1 或高时,与门的输出才为逻辑 1 或高。
下表表示三输入与门 −
的真值表| 输入 | 输出 | ||
|---|---|---|---|
| A | B | C | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
该真值表显示,只有当与门的所有三个输入都为高电平或逻辑 1 时,输出才为高电平或逻辑 1。对于其他输入组合,输出为低电平或逻辑 0。
从这些与门真值表中,我们可以得出结论,只有当所有输入都为高电平或逻辑 1 时,与门才会产生高电平或逻辑 1 输出,否则输出为低电平或逻辑 0。
与门的工作原理
下面解释了双输入与门的工作原理 −
- 如果 A = 0 且 B = 0,则输出为低电平,即 Y = 0。
- 如果 A = 0 且 B = 1,则输出为低电平,即 Y = 0。
- 如果 A = 1 且 B = 0,则输出为低电平,即 Y = 0。
- 如果 A = 1 且 B = 1,则输出为高,即 Y = 1。
三输入与门的工作原理如下 −
- 如果 A = 0、B = 0 且 C = 0,则输出为低,即 Y = 0。
- 如果 A = 0、B = 0 且 C = 1,则输出为低,即 Y = 0。
- 如果 A = 0、B = 1 且 C = 0,则输出为低,即 Y = 0。
- 如果 A = 0、B = 1 且 C = 1,则输出为低,即 Y = 0。
- 如果 A = 1、B = 0 且 C = 0,输出为低,即 Y = 0。
- 如果 A = 1、B = 0 和 C = 1,则输出为低,即 Y = 0。
- 如果 A = 1、B = 1 和 C = 0,则输出为低,即 Y = 0。
- 如果 A = 1、B = 1 和 C = 1,则输出为高,即 Y = 1。
这都是关于双输入和三输入与门的工作原理。
与门的布尔表达式
布尔表达式是一个逻辑方程或逻辑函数,表示与门的输入和输出之间的数学关系。
双输入与门的布尔表达式由以下公式给出:
Y = A · B
其中,A 和 B 为输入,Y 为输出。此表达式读作"Y 等于 A AND B"。点 (·) 符号表示 AND 运算。
对于三输入 AND 门,布尔表达式由以下公式给出:
Y = A · B · C
读作"Y 等于 A AND B AND C"。
同样,我们可以得到具有任意数量输入变量的 AND 门的布尔表达式。
使用晶体管的 AND 门
下图显示了双输入 AND 门的晶体管电路。
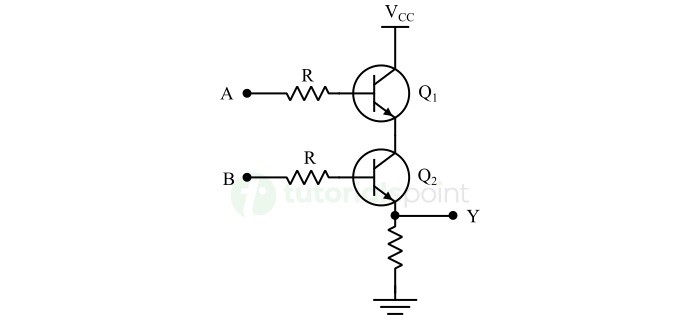
使用晶体管实现 AND 门需要的晶体管数量与输入数量相同。例如,双输入 AND 门需要两个晶体管。
晶体管 AND 门的工作原理
下面解释了上图所示的晶体管 AND 门的工作原理−
当输入 A 和 B 都为低电平时,晶体管 Q1 和 Q2 保持关闭状态并充当打开开关。因此,输出线 Y 将直接连接到地电位。因此,输出为低电平或逻辑 0。
当输入 A 为低电平且输入 B 为高电平时,第一个晶体管 Q1 关闭,第二个晶体管 Q2 导通。但电源电压仍不会连接到输出线,输出线将保持在地电位。因此,输出为低电平或逻辑 0。
当输入 A 为高电平且输入 B 为低电平时,晶体管 Q1 将导通,晶体管 Q2 将保持关闭。在这种情况下,输出线不接收电源电压,而是连接到地电位。因此,对于这种输入组合,输出为低或逻辑 0。
当输入 A 和 B 都为高时,晶体管 Q1 和 Q2 都将打开并充当闭合开关。在这种情况下,电源电压直接连接到输出线。这使电路的输出为高或逻辑 1。
这就是上述晶体管电路充当双输入与门的方式。我们可以添加更多晶体管来实现高阶与门。
使用开关的与门
我们还可以使用电池、开关和灯或灯泡来实现与门逻辑。下图显示了使用开关的与门。
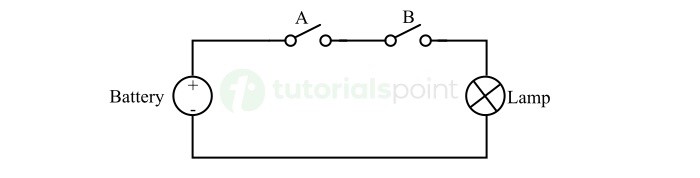
在这个与门电路中,我们有一个电压源,两个开关代表与门的两个输入端,还有一个灯代表输出。
从电路中,我们可以看到,如果开关 A 和 B 都闭合,则电路中将有一个闭合点,电流将流过电路。因此,灯将发光,代表高或逻辑 1 输出。
如果两个开关都打开或任何一个打开,电流路径将中断,使灯熄灭。这代表与门输出的低或逻辑 0 状态。
这样,上面描绘的开关电路执行与门操作。通过增加更多串联开关,我们可以实现更高阶的与门。
与门 IC
在实践中,有一种集成电路,即 IC 7408,它是最常用的与门 IC。此与门 IC 采用晶体管-晶体管逻辑 (TTL) 实现。下图显示了与门 IC 7408 的框图。
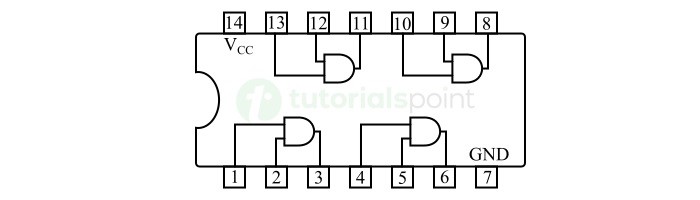
它是一个四路 2 与门 IC,在单个芯片上集成了四个双输入与门。它有 14 个引脚。
结论
总之,与门是数字电路中用于实现布尔乘法函数的基本逻辑门。
只有当所有输入都为高电平或逻辑 1 时,与门的输出才为高电平或逻辑 1。否则,它会产生低电平或逻辑 0 输出。
与门在数据处理、存储设备、算术逻辑单元、控制系统等各种数字电子应用中发挥着重要作用。


