可编程逻辑阵列 (PLA)
在本章中,我们将讨论可编程逻辑阵列 (PLA)、其框图和应用。可编程逻辑阵列 (PLA) 是一种可编程逻辑器件 (PLD)。从历史上看,PLA 是第一个 PLD 器件。它包含一个 AND 和 OR 门阵列/矩阵,其配置根据应用需求完成。
在 PLA 中,一组熔断器用于建立或移除 AND 运算中文字的接触或 OR 运算中乘积项的接触。因此,PLA 是一种允许 AND 矩阵和 OR 矩阵编程的 PLD。
在数字电子技术中,PLA 用于设计和实现各种复杂的组合电路。但是,一些 PLA 还具有存储元件,因此它们也可用于实现顺序电路。
PLA 框图
可编程逻辑阵列 (PLA) 是一种固定架构可编程逻辑器件 (PLD),由可编程 AND 门和 OR 门组成。 PLA 包含一个可编程的 AND 数组,后面跟着一个可编程的 OR 数组。
PLA 的框图如下图所示 −
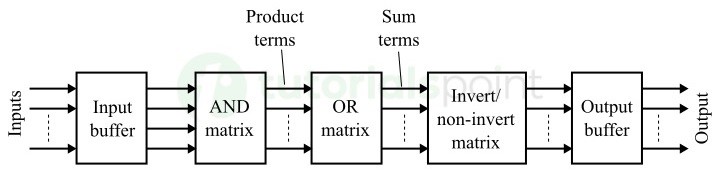
它由以下主要组件组成 −
输入缓冲器
PLA 中使用输入缓冲器来避免对驱动输入的源产生负载效应。
AND 数组/矩阵
PLA 中使用 AND 数组/矩阵来生成乘积项。
OR 数组/矩阵
在 PLA 中,OR 数组/矩阵用于生成所需的输出。这是通过将乘积项进行"或"运算以产生和项来实现的。
反转/非反转矩阵
它是 PLA 中使用的缓冲器,用于将输出设置为高电平有效或低电平有效。
输出缓冲器
此缓冲器用于输出端。它主要用于提高可编程逻辑阵列 (PLA) 的驱动能力。
使用 PLA 进行组合逻辑设计
在数字电子领域,PLA 广泛用于设计组合逻辑电路。使用 PLA 设计组合电路的最大优势在于 PLA 由可编程 AND 和 OR 阵列组成,可以实现自定义所需的逻辑功能。
下面将介绍使用 PLA 设计组合逻辑电路的分步过程 −
步骤 1 − 开发一个 PLA 程序表,显示输入、乘积项和输出。
步骤 2 − 设计可以生成所需乘积项的 AND 矩阵。
步骤 3 − 设计可以生成所需输出的 OR 矩阵。
步骤 4 − 设计反相/非反相矩阵以设置低电平有效或高电平有效输出。
步骤 5 −最后,利用 PLA 程序表对 PLA 进行编程。
让我们借助一个例子来了解使用 PLA 进行组合电路设计的过程。
示例
使用可编程逻辑阵列 (PLA) 设计全加器电路。
解决方案
全加器由三个输入和两个输出组成。由于它有 3 个输入,因此总共有 8 个乘积项,它们在全加器的以下真值表中给出 −
| 输入 | 输出 | |||
|---|---|---|---|---|
| A | B | Cin | S | Cout |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
从该真值表可知,输出和 (S) 和输出进位 (Cout) 的计算公式为:
$$\mathrm{S \: = \: \sum \: m(1,2,4,7)}$$
$$\mathrm{C_{out} \: = \: \sum \: m(3,5,6,7)}$$
因此,它们的布尔表达式为:
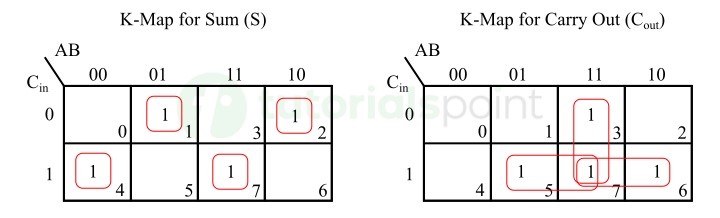
$$\mathrm{S \: = \: \overline{A} \: B \: \overline{C_{in}} \: + \: \overline{A} \: \overline{B} \: C_{in} \: + \: A \: \overline{B} \: \overline{C_{in}} \: + \: A \: B \: C_{in}}$$
$$\mathrm{C_{out} \: = \: A \: B \: + \: B \: C_{in} \: + \: A \: C_{in}}$$
从这两个布尔表达式可以看出有七个乘积项和两个求和项。此全加器电路的 PLA 程序表如下所示 −
| Sr.No | 乘积项 | 输入 | 输出 | |||
|---|---|---|---|---|---|---|
| A | B | Cin | S | Cout | ||
| 1 | $\mathrm{\overline{A} \: B \: \overline{C_{in}}}$ | 0 | 1 | 0 | 1 | - |
| 2 | $\mathrm{\overline{A} \: \overline{B} \: C_{in}}$ | 0 | 0 | 1 | 1 | - |
| 3 | $\mathrm{A \: \overline{B} \: \overline{C_{in}}}$ | 1 | 0 | 0 | 1 | - |
| 4 | $\mathrm{A \: B \: C_{in}}$ | 1 | 1 | 1 | 1 | - |
| 5 | $\mathrm{A \: B }$ | 1 | 1 | - | - | 1 |
| 6 | $\mathrm{B \: C_{in}}$ | - | 1 | 1 | - | 1 |
| 7 | $\mathrm{A \: C_{in}}$ | 1 | - | 1 | - | 1 |
| T | T | |||||
在此 PLA 程序表中,"1"代表连接,"-"代表输出中没有乘积项。"T"代表真,它代表高电平有效输出。
全加器的 PLA 电路图如下图所示。
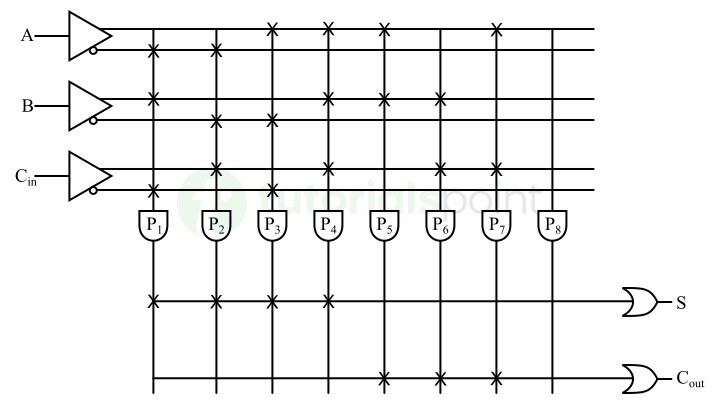
此示例说明了使用 PLA 实现组合逻辑电路的完整分步过程。
PLA 的优势
以下是可编程逻辑阵列 (PLA) 的一些关键优势,这些优势使其在数字电子领域不可或缺 −
- PLA 在设计和实现各种数字逻辑操作方面提供了灵活性。 PLA 可用于实现满足不同应用需求所需的自定义逻辑功能。
- PLA 还可最大限度地缩短设计和开发新数字电路或系统所需的时间。
- PLA 提供了一种实现高度复杂数字逻辑功能的较便宜方法。PLA 无需分立元件即可实现逻辑功能,因此可提高空间效率。
- 由于 PLA 是可编程的,因此无需重新制造整个电路即可修改其设计。
PLA 的缺点
然而,PLA 具有如上所述的几个优点。但它们也有一些缺点,如下所示 −
- 对于大量输入和输出,PLA 的设计和实现非常复杂。作为固定架构设备,PLA 在速度和处理能力方面性能有限。
- PLA 通常针对特定应用进行优化,因为它具有固定数量的 AND 门和 OR 门。此限制不允许设计人员使用同一 PLA 实现高度复杂的逻辑功能。
- 对 PLA 进行编程是一个耗时且复杂的过程。
PLA 的应用
可编程逻辑阵列 (PLA) 广泛应用于不同领域的各种应用中。以下是 PLA 的一些常见应用 −
- PLA 用于数字信号处理领域,以实现各种逻辑功能,例如滤波、卷积、傅里叶变换等。
- 在控制系统中,PLA 用于实现各种组件(如反馈、PID 控制器、状态机等)的控制逻辑功能。
- PLA 用于执行不同类型的算术运算,如加法、减法、乘法和除法。
- PLA 还可应用于数据压缩和加密技术领域。 PLA 用于数字通信系统和网络设备,以实现协议处理、数据包处理、错误检测和纠正等算法。
- PLA 还用于不同的测量仪器,如数字示波器、协议分析仪、逻辑分析仪等。
结论
PLA 只不过是一种数字逻辑设备,用于实现复杂的数字功能,而无需使用与门、或门等分立元件。在本章中,我们解释了可编程逻辑阵列 (PLA) 的基础知识和应用。


