使用 8:1 多路复用器的三变量函数
本章首先,让我们对 8:1 多路复用器进行基本介绍,然后再介绍如何使用 8:1 多路复用器实现三变量逻辑函数。
8:1 多路复用器简介
多路复用器(或 MUX)是一种数字逻辑电路,它接受多个数据输入,但每次只允许其中一个数据通过输出线。因此,多路复用器也称为 数据选择器。换句话说,多路复用器是一种数字电路,
根据输入数据线的数量,有几种类型的多路复用器。但是,本文旨在解释如何使用 8:1 多路复用器实现三个变量的逻辑函数。因此,我们只讨论 8:1 多路复用器的基础知识。
8:1 多路复用器具有八条输入数据线,即 I0、I1、I2、…I7,三条选择线,即 S0、S1 和 S2,以及一条输出线 Y。8:1 多路复用的框图如图 1 所示。
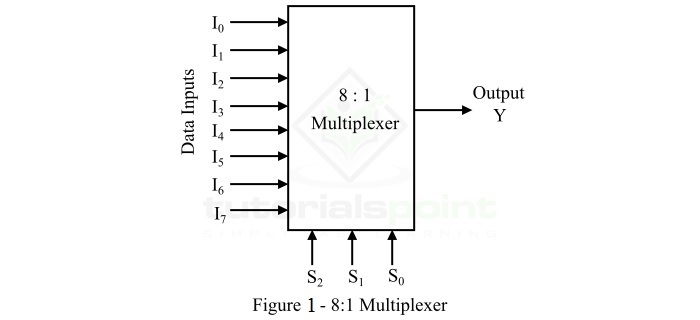
应用于三条选择线的逻辑电平决定哪些数据输入通过多路复用器的输出通道。借助下面给出的真值表,可以理解 8:1 多路复用器的操作。
| 选择行 | 输出 | ||
|---|---|---|---|
| S2 | S1 | S0 | Y |
| 0 | 0 | 0 | I0 |
| 0 | 0 | 1 | I1 |
| 0 | 1 | 0 | I2 |
| 0 | 1 | 1 | I3 |
| 1 | 0 | 0 | I4 |
| 1 | 0 | 1 | I5 |
| 1 | 1 | 0 | I6 |
| 1 | 1 | 1 | I7 |
现在,让我们借助一个示例讨论如何使用 8:1 多路复用器实现三变量逻辑函数。
示例
使用 8:1 多路复用器实现以下逻辑函数。
$$\mathrm{F \lgroup A,B,C \rgroup \: = \: \sum m \lgroup 0,1,2,5,7 \rgroup }$$
解决方案
给定逻辑函数的 8:1 多路复用器的真值表如下 −
| 选择行 | 输出 | ||
|---|---|---|---|
| S2 | S1 | S0 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
利用该真值表,我们可以绘制逻辑框图,使用图 2 所示的 8:1 MUX 实现函数 F。
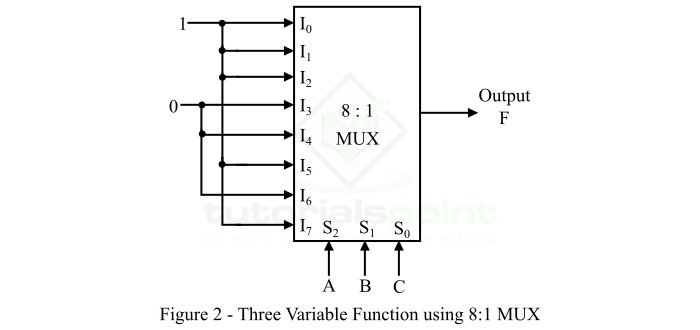
此处,输入 A、B 和 C 分别应用于选择线 S2、S1 和 S0。从真值表可知,当 ABC = 000、001、010、101、111 时,函数 F = 1。因此,我们将逻辑 1 连接到数据输入线 I0、I1、I2、I5 和 I7,将逻辑 0 连接到所有其他数据输入线,即 I3、I4 和 I6。
结论
通过这种方式,我们可以轻松地使用 8:1 多路复用器实现给定的 3 变量布尔函数。为了在使用 8:1 MUX 实现三变量布尔运算方面表现出色,请尝试解决以下教程问题。
解决问题
Q1. − 使用 8 对 1 MUX 实现以下布尔函数。
$$\mathrm{F\lgroup X,Y,Z \rgroup \: = \: \sum m \lgroup 0,2,5,7 \rgroup}$$
Q2. −使用 8:1 多路复用器实现以下三变量逻辑函数。
$$\mathrm{F \lgroup A,B,C \rgroup \: = \: \sum m \lgroup 0,1,3,4,6 \rgroup}$$


