奇偶校验位生成器和校验器
在数字电子领域,确保数据完整性非常重要。为此,我们有两个数字电路,即奇偶校验生成器和奇偶校验器。这两个电路都有助于我们检测和纠正传输数据中的任何错误。
阅读本章以了解奇偶校验生成器和奇偶校验器的基础知识,以及它们的类型和应用。
什么是奇偶校验位?
在数字信号处理中,在原始二进制或数字代码中添加一个额外的位 0 或 1,以检测和纠正传输过程中可能发生的任何数据错误。这个额外的位称为奇偶校验位。
在原始数字代码中添加奇偶校验位会使代码中的 1 总数为偶数或奇数。因此,根据数据中 1 的数量,奇偶校验可分为两种类型,即 偶校验 和 奇校验。
如果我们在原始二进制代码中添加 0 或 1,使得代码中 1 的总数为偶数,则称为偶校验。
另一方面,如果我们在原始二进制代码中添加奇偶校验位,即 0 或 1,使得代码中 1 的总数为奇数,则称为奇校验。
奇偶校验位是数字电子技术中使用的最简单的错误检测技术之一。
奇偶校验位如何工作?
现在让我们考虑一个例子来了解奇偶校验位的工作原理。
假设我们有一个十进制数,比如 5,它的BCD码是0101。这个代码的1的总数是偶数,因为它有两个1。
在偶校验的情况下,我们在原始代码中添加一个校验位0,使代码中的1的数量为偶数。
因此,添加偶校验后,我们得到01010。这里,在原始代码的末尾添加了一个0(校验位)。
如果我们需要执行奇校验,那么我们在原始代码的末尾添加一个1,我们得到01011。现在,代码中1的总数(包括校验位)是奇数,即三个1。这确保了它是奇校验方案。
下表显示了从 0 到 9 的十进制数字的奇校验位和偶校验位 −
| 十进制数字 | BCD | 偶校验 | 奇校验 |
|---|---|---|---|
| 0 | 0 0 0 0 | 0 | 1 |
| 1 | 0 0 0 1 | 1 | 0 |
| 2 | 0 0 1 0 | 1 | 0 |
| 3 | 0 0 1 1 | 0 | 1 |
| 4 | 0 1 0 0 | 1 | 0 |
| 5 | 0 1 0 1 | 0 | 1 |
| 6 | 0 1 1 0 | 0 | 1 |
| 7 | 0 1 1 1 | 1 | 0 |
| 8 | 1 0 0 0 | 1 | 0 |
| 9 | 1 0 0 1 | 0 | 1 |
当接收端接收到数字信号时,如果在偶校验方案中 1 的总数为奇数,或在奇校验方案中 1 的总数为偶数,则奇偶校验电路会生成错误信号。
奇偶校验位错误检测技术的主要限制是它只能检查单比特错误,而不能检查多比特错误。
什么是奇偶校验发生器?
能够根据原始数字代码生成奇偶校验位的组合逻辑电路称为奇偶校验位发生器或奇偶校验发生器。
奇偶校验发生器用于发送端,在传输之前生成奇偶校验位并将其添加到原始代码中。
首先,奇偶校验发生器读取输入数据并据此计算奇偶校验位。生成奇偶校验位后,将其添加到原始数据代码中。这样会给出一个输出代码,该代码是原始代码加上新生成的奇偶校验位。
奇偶校验生成器的类型
根据所使用的奇偶校验系统,有两种主要类型的奇偶校验生成器 −
- 偶校验生成器
- 奇校验生成器
让我们详细讨论偶校验和奇校验生成器。
偶校验生成器
偶校验生成器是一种奇偶校验生成器,其中将奇偶校验位(0 或 1)添加到原始数据中,以便最终数字代码包含偶数个 1,包括奇偶校验位。
因此,我们可以说,偶校验生成器输出中的 1 总数(包括奇偶校验位)是偶数。
在偶校验生成器的情况下 −
- 如果数字代码包含奇数个 1,则偶校验生成器将生成 1 作为校验位以维持偶校验。
- 如果数字代码已经包含偶数个 1,则偶校验生成器将生成 0 作为校验位以维持偶校验。
例如,考虑数字代码 0110。此代码已经包含偶数个 1。因此,如果将其输入到偶校验生成器,校验生成器的输出将为 01100。其中,LSB 0 是偶校验生成器添加的校验位。
类似地,考虑另一个数字代码 0111。在这种情况下,代码中的 1 总数为三个(奇数)。如果我们将此代码输入到偶校验生成器,生成器的输出将为 01111,包含偶数个 1。其中,LSB 1 是校验位。
现在让我们设计一个 4 位偶校验生成器。以下是 4 位偶校验生成器的真值表 −
| 4 位代码 | 偶校验 | |||
|---|---|---|---|---|
| A | B | C | D | P |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
通过简化真值表,可以得到 4 位偶校验发生器的布尔表达式,真值表如下所示。
$$\mathrm{P \: = \: A \: \oplus \: B \: \oplus \: C \: \oplus \: D}$$
下图为 4 位偶校验发生器的逻辑电路图。
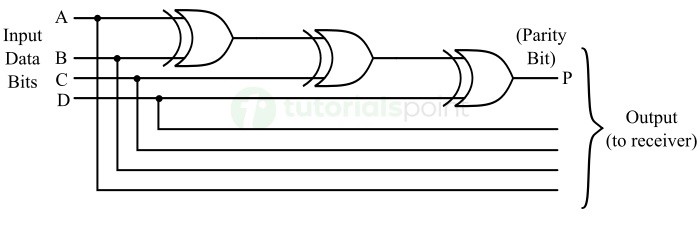
在该电路中,三个 XOR 门连接在一起,将输入代码的四个数据位相加。输出产生的总和位将是奇偶校验位。
这就是偶校验发生器及其功能的全部内容。
奇校验发生器
一种将奇偶校验位添加到二进制代码的奇偶校验发生器,使得输出代码中的 1 的总数为奇数,它被称为奇校验发生器。
奇校验发生器的输出是包含奇数个 1 的数字代码,包括奇偶校验位。
对于奇校验发生器,
- 如果原始数据包含偶数个 1,则奇校验发生器将 1 作为奇偶校验位添加到原始代码以保持奇校验。
- 如果原始数据已经包含奇数个 1,则奇校验发生器将 0 作为奇偶校验位添加到原始代码原始代码以保持奇校验。
让我们借助示例来了解奇校验生成器的功能。
考虑一个 4 位数字代码 0110。此代码具有偶数个 1(两个)。因此,如果我们将此代码输入到奇校验生成器,生成器将添加一个 1 并产生代码 01101 作为输出。此结果代码具有奇数个 1,包括校验位,并确保奇校验系统。
同样,考虑另一个 4 位代码 0111。此代码已经包含奇数个 1,即三个 1。因此奇校验发生器将为其添加一个0作为校验位,并给出输出代码01110,以确保奇校验系统。
以下是4位奇校验发生器的真值表−
| 4位代码 | 奇校验 | |||
|---|---|---|---|---|
| A | B | C | D | P |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
4 位奇校验发生器的布尔表达式为,
$$\mathrm{P \: = \: \overline{A \: \oplus \: B \: \oplus \: C \: \oplus \: D}}$$
下图为 4 位奇校验发生器的逻辑电路图。
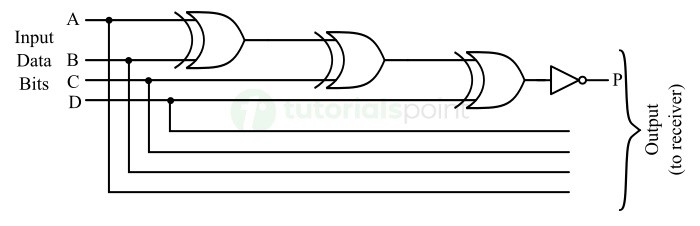
在该电路中,三个 XOR 门连接在一起,将输入数据的四位相加,然后对和位求补,得到奇校验位。
以上就是偶校验发生器和奇校验的全部内容奇偶校验发生器。这两种类型的奇偶校验发生器都用于数字系统,根据应用的需求实现不同类型的奇偶校验系统。
奇偶校验发生器广泛用于数字通信和存储系统,以检查数据传输过程中可能发生的错误。
什么是奇偶校验器?
通过分析奇偶校验位来检查和验证传输数据正确性的组合电路称为奇偶校验器。奇偶校验器的主要功能是检测数据传输过程中可能发生的错误。
奇偶校验器用于通信信道的接收端。它从通信信道接收传输的数据。该数据包括原始消息代码和奇偶校验位。
之后,奇偶校验器计算数据代码中的 1 的数量,并将该数字与预期代码进行比较,以确定是否存在任何错误。如果接收的数据有任何错误,奇偶校验器将采取适当的措施,如请求重新传输数据。
奇偶校验器是数字通信系统中确保数据正确性和完整性的重要组成部分。它还提供了一种简单有效的错误检测方法。
奇偶校验器的类型
根据所使用的奇偶校验系统,有两种主要类型的奇偶校验器 −
- 偶校验器
- 奇校验器
让我们详细讨论每种类型的奇偶校验器。
偶校验器
根据偶校验系统验证接收数据是否正确的奇偶校验器类型称为偶校验器。
偶校验器计数并验证接收的数据是否包含偶数个 1,包括奇偶校验位。
因此,在偶校验器的情况下,
- 如果接收数据中的 1 的数量为偶数,则认为数据无错误。
- 如果接收数据中的 1 的数量为奇数,则奇偶校验器显示数据包含一些错误。
偶校验器如何工作?
让我们借助示例来了解偶校验。
考虑一个 4 位数字代码 00110(在 LSB 位置有 0 作为奇偶校验位),此代码由偶校验器接收。奇偶校验器将计算代码中偶数(两个)1 的数量。因此,奇偶校验器显示它是一个无错误代码,其中 LSB 0 是奇偶校验位。
同样,考虑另一个 4 位消息代码 01011,其 LSB 位置有一个奇偶校验位。此代码包含奇数个 1(三个 1)。因此,偶校验器将显示代码存在一些错误。
现在让我们实现一个 4 位偶校验器,其真值表如下所示 −
| 带奇偶校验的 4 位代码 | 偶校验 | ||||
|---|---|---|---|---|---|
| A | B | C | D | P | CP |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
这里,位 ABCD 代表原始数字代码,P 是奇偶校验位。
在这个真值表中,如果 CP = 1,则接收的代码将出现错误。如果 CP = 0,则接收代码中没有错误。
4 位偶校验器的布尔表达式为,
$$\mathrm{C_{P} \: = \: A \: \oplus \: B \: \oplus \: C \: \oplus \: D \: \oplus \: P}$$
4 位偶校验器的逻辑电路图如下图所示。

奇校验校验器
奇校验器是一种组合逻辑电路,用于根据奇校验系统检查和验证接收到的数据是否正确。
奇校验器计数并确认接收到的数据包含奇数个 1(包括校验位)。
对于奇校验器,
- 如果接收到的代码中的 1 的数量为奇数,则代码中没有错误。
- 如果接收到的代码中的 1 的数量为偶数,则表示传输过程中可能发生的代码错误。
例如,考虑一个 4 位数据代码 01101(LSB 1 是校验位)。在此代码中,1 的数量为奇数(三个)。因此,奇校验器将显示代码无错误。
同样,考虑另一个 4 位数据代码 01100(LSB 0 是奇偶校验位)。此代码包含偶数个 1,即只有两个 1。在这种情况下,奇校验器将显示代码有错误。
现在让我们实现一个 4 位奇校验器,其真值表如下所示。
| 带奇偶校验的 4 位代码 | 奇校验 | ||||
|---|---|---|---|---|---|
| A | B | C | D | P | CP |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 |
在此真值表中,位 ABCD 代表原始二进制代码,P 是奇偶校验位。
从此真值表中,我们可以观察到,如果 CP = 1,则代码包含偶数个 1,因此传输过程中代码中发生了错误。
如果 CP = 0,则代码包含奇数个 1,这表示代码没有错误。
这里给出了 4 位奇校验器的布尔表达式,
$$\mathrm{C_{P} \: = \: \overline{A \: \oplus \: B \: \oplus \: C \: \oplus \: D \: \oplus \: P}}$$
下图为该 4 位奇校验器的逻辑电路图。
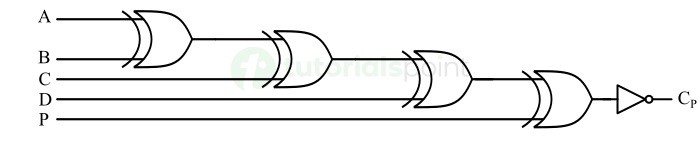
IC 74180 9 位奇校验发生器/校验器
奇校验发生器/校验器 IC 是一种小型设备,用于检测通过通信信道传输的数据流中的错误。市场上有几种不同的奇偶校验发生器/校验器 IC,但最常用的是 74180 IC。
74180 奇偶校验发生器/校验器 IC 是一种 9 位奇偶校验发生器或校验器设备,用于高速数据传输系统中检测错误。
奇偶校验发生器/校验器 IC 74180 的引脚图如下图所示。
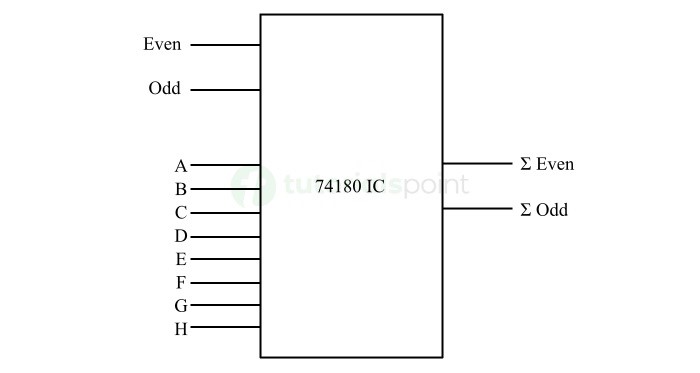
它由从 A 到 H 标记的八条输入线、两条标记为"偶数"和"奇数"的级联输入线以及两条指定为"偶数和"和"奇数和"的输出线组成。
根据所选的操作模式,IC 74180 可以用作奇偶校验发生器或奇偶校验校验器。
现在让我们考虑一个例子来了解奇偶校验发生器/校验器 IC 如何工作?
如果 IC 74180 作为偶校验校验器运行,并且接收的数据中存在奇偶校验错误。在这种情况下,输出"偶数和"将为低,输出"奇数和"将为高。
如果 IC 74180 作为奇校验器运行,并且数据流中发生错误。输出"奇数和"将为低,而输出"偶数和"将为高。
这就是关于奇偶校验发生器或校验器 IC 74180 的全部内容。现在让我们讨论奇偶校验发生器/校验器的应用。
奇偶校验发生器和校验器的应用
在数字系统中,如数字通信和存储系统,奇偶校验发生器和校验器是提供在传输和检索的数据流中进行错误检测和纠正的强大方法的基本组件。因此,奇偶校验发生器/校验器有助于确保数字数据的完整性、可靠性和安全性。
以下示例说明了奇偶校验发生器和校验器在各种数字电子应用中的应用 −
- 在数字通信系统中,奇偶校验发生器和校验器用于确保传输和接收数据的完整性和准确性。奇偶校验发生器和校验器有助于检测数据中的错误,这些错误可能是由于通信信道传输过程中的噪声和干扰引起的。
- 奇偶校验发生器和校验器用于存储系统(如 RAM 和 ROM)中,以检测存储和检索的数据中的错误。
- 在数字网络中,奇偶校验发生器和校验器用于提高数据传输的可靠性并验证传输数据的正确性。
- 奇偶校验发生器和校验器用于工业自动化和控制系统,以确保工业系统的准确可靠运行。
- 奇偶校验发生器和校验器还用于医疗设备,用于诊断和监测患者的健康状况,避免医疗报告和诊断数据中出现任何类型的错误。
结论
奇偶校验发生器是一种组合逻辑电路,用于生成和添加奇偶校验器是用于对输入或传输的数据进行奇偶校验的组合电路,而奇偶校验器也是用于验证接收数据正确性的组合电路。
奇偶校验发生器用于发送器电路,奇偶校验器用于接收器电路。这两个电路共同用于确保各种数字系统中数据的可靠性、完整性和准确性。


