逻辑电平和脉冲波形
数字系统是一种利用二进制数字系统工作的电子系统。换句话说,数字系统是一种双态电子系统,用于表示两个二进制数字 0 和 1,其中 0 表示系统的低或"关闭"状态,而 1 表示系统的高或"打开"状态。
在数字电子领域,不同的电压电平用于表示数字信号中的两个二进制值,即 0 和 1。这些电压电平称为逻辑电平。
在本章中,我们将学习逻辑电平和脉冲波形的概念。
什么是逻辑电平?
在数字电子技术中,表示特定二进制值 0 或 1 的电压电平称为逻辑电平。这里,二进制值 0 表示低电平,而二进制值 1 表示高电平。
因此,逻辑电平可分为以下两种类型 −
- 高逻辑电平
- 低逻辑电平
让我们详细讨论一下这两种逻辑电平。
高逻辑电平
在数字系统中,接近系统可以处理而不会损坏的最大电压电平的电压电平称为高逻辑电平。
高逻辑电平用二进制数字"1"表示。高逻辑电平的电压电平取决于用于设计系统的技术标准。通常,2 V 和 5 V 之间的电压值代表高逻辑电平或 1。
低逻辑电平
在数字系统中,低逻辑电平定义为系统保持关闭状态的最大电压电平。
低逻辑电平用二进制数字"0"表示。与高逻辑电平类似,低逻辑电平的电压电平取决于用于设计系统的技术标准。在实际操作中,0 V 和 0.8 V 之间的电压值代表低逻辑电平或逻辑 0。
在大多数实际数字系统中,接地电压用于表示低逻辑电平。
注意 − 电压值 0.8 V 和 2 V 之间的电压范围称为不确定逻辑范围。如果数字信号介于 0.8 和 2 V 之间,则系统的响应是不可预测的。
什么是脉冲?
脉冲是一种电子信号,可以在两种可能的状态(即高状态和低状态)之间突然改变。
用于表示脉冲转换的图形称为脉冲波形。脉冲在数字系统、通信系统以及许多其他电子设备和电路的运行中非常重要。
根据开关特性,脉冲可分为以下两种类型 −
- 正脉冲 −当信号正常地从低逻辑电平变为高逻辑电平,然后返回到其正常的低逻辑电平时,则称为正脉冲。
- 负脉冲 − 当信号正常地从高逻辑电平变为低逻辑电平,然后返回到其正常的高逻辑电平时,则称为负脉冲。
正脉冲和负脉冲的脉冲波形如下图所示。
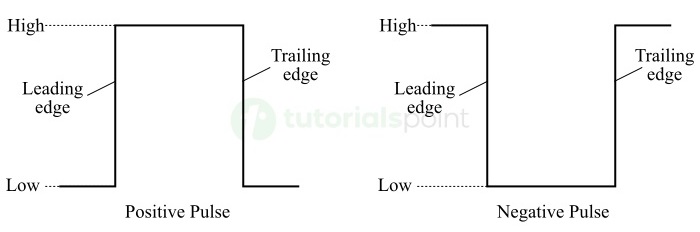
脉冲有两个边沿,分别为前沿和后沿。
对于正脉冲,从低逻辑电平到高逻辑电平的边沿称为前沿,从高逻辑电平到低逻辑电平的边沿称为后沿。
对于负脉冲,从高逻辑电平到低逻辑电平的边沿称为前沿,从低逻辑电平到高逻辑电平的边沿称为后沿。
上图所示的正、负脉冲波形是理想脉冲波形,因为它们的前沿和后沿是瞬时变化的,即在零时间内。但在实际操作中,脉冲的边沿不会瞬间从低逻辑电平变为高逻辑电平或从高逻辑电平变为低逻辑电平。
需要有限时间从低逻辑电平变为高逻辑电平和反之亦然的脉冲波形被称为非理想脉冲波形。

在非理想脉冲波形的情况下,脉冲从低逻辑电平变为高逻辑电平所需的时间称为上升时间。脉冲从高逻辑电平变为低逻辑电平所用的时间称为下降时间。
脉冲波形的类型
数字系统中使用的脉冲波形主要分为以下两种类型 −
周期波形
以规则的时间间隔重复的脉冲波形称为周期波形。完成一个周期所用的时间称为周期波形的时间周期。
非周期波形
不以规则的时间间隔重复的脉冲波形称为非周期或非周期波形。
结论
总之,"逻辑电平"是数字系统中用来表示系统状态的概念。数字系统中有两种可能的逻辑电平,即高逻辑电平和低逻辑电平。高逻辑电平用二进制 1 表示,而低逻辑电平用二进制 0 表示。
数字信号或脉冲的图形表示称为"脉冲波形"。脉冲波形用于表示脉冲或数字信号的转换或数字系统的状态。在本章中,我们讨论了逻辑电平和脉冲波形的概念。在下一章中,我们将学习"数字系统的组成部分"。


