使用布尔代数进行简化

什么是卡诺图 (K-Map)?

K-Map 是一种图形工具，用于简化以标准形式表示的布尔表达式以获得其最小形式。

K-Map 基本上是由相邻单元格或方块排列组成的图形或图表，其中每个单元格代表函数变量的特定组合，可以是总和形式，也可以是乘积形式。

K-Map 中的单元格数量取决于布尔函数中的变量数量，即 K-map 有 2ⁿ 个相邻单元格，其中 n 是布尔表达式中的变量数量。因此，2 变量 K-map 中的单元格数量为 4 (2²)，3 变量 KMap 中的单元格数量为 8 (2³)，4 变量 K-map 中的单元格数量为 16 (2⁴)，依此类推。

但是，我们可以将 K Map 用于任意数量的变量。但是，对于简化变量超过 5 个的布尔函数，它变得很繁琐。

现在，让我们讨论使用 K-Map 简化布尔表达式的过程。

使用 K Map 简化布尔表达式的步骤

以下步骤涉及使用 K-Map − 简化给定的布尔表达式

步骤 1 −根据给定布尔函数中的变量数量选择 K-Map。

步骤 2 − 识别最小项(SOP 形式)或最大项(POS 形式)。

步骤 3 − 对于 SOP(乘积和)形式，根据给定函数的最小项，将 1 放入 K-Map 的单元格中。按照以下方式读取 K-Map −

• 读取不与其他 1 相邻的 1 的 K-map。这些 1 是孤立的最小项，因此应按原样读取，因为它们不能组合在一起。
• 读取仅与另一个 1 相邻的 1 的 K-map。将这些最小项组合成 2 个方格。
• 读取相邻 1 的四元组(4 个方格)、八元组(8 个方格)等的 K-map，即使它们中的一些 1 已经组合成其他组。唯一要记住的是，它们必须在几何上形成一个矩形或正方形。
• 读取 K-map 中任何尚未分组的 1，并尽可能将它们分组为更大的正方形或矩形。
• 最后，获得所有组的乘积项，然后将它们相加以形成最小 SOP 表达式。

对于 POS(和的乘积)形式，根据给定函数的最大项将 0 放入 K-Map 的单元格中。按如下方式读取 K-Map −

• 读取不与其他 0 相邻的 0 的 K-map。这些 0 是孤立的最大项，因此应按原样读取，因为它们不能组合在一起。
• 读取仅与另一个 0 相邻的 0 的 K-map。将这些最大项组合成 2 个方格。
• 读取相邻 0 的四元组(4 个方格)、八元组(8 个方格)等的 K-map，即使它们中的一些 0 已经组合成其他组。唯一要记住的是，它们必须在几何上形成一个矩形或正方形。
• 读取 K-map 中尚未组合的任何 0，并尽可能将它们组合成更大的正方形或矩形。
• 最后，获得所有组的和项，然后将它们相乘以形成最小 POS 表达式。

让我们借助一些已解决的示例来理解使用 K-map 简化布尔表达式的过程。

示例 1

使用 K-Map 以 SOP 形式简化以下 3 变量布尔函数。

$$\mathrm{F(P, \: Q, \:R) \: = \: \sum m ( 0, \: 1, \: 3, \: 5, \: 7)}$$

解决方案

给定布尔函数的 K-Map 表示如图 1 所示。

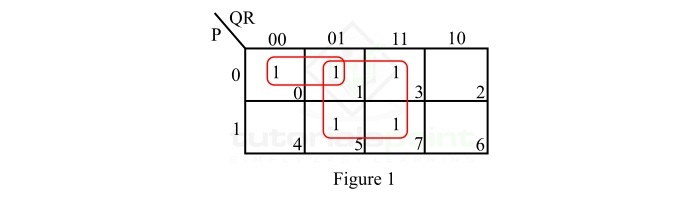
此 K-map 的简化按照以下步骤进行 −

• 没有孤立的 1。
• 最小项 m₁ 与最小项 m₃、m₅ 和 m₇ 形成一个 4 平方。将其制作并读作 R。
• 最小项 m₀ 与最小项 m₁ 形成一个 2 平方。将其写成并读作 $\mathrm{\bar{P} \: \bar{Q}}$
• 将所有乘积项写成 SOP 形式。

因此，简化的 SOP 表达式为，

$$\mathrm{F \: = \: R \: + \: \bar{P}\bar{Q}}$$

示例 2

使用 K-Map 简化 POS 形式的以下 3 变量布尔函数。

$$\mathrm{F(A, \: B, \: C) \: = \: \Pi \: M(1, \: 2, \: 4, \: 6)}$$

解决方案

给定布尔函数的 POS K-map 表示如图 2 所示。

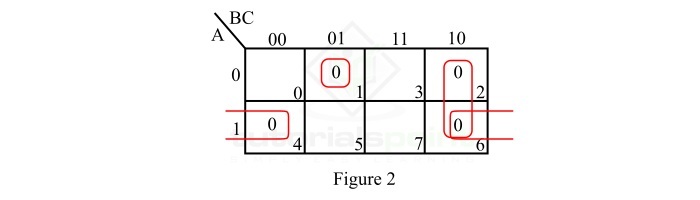
此 POS K-map 的简化按照以下步骤进行 −

• 最大项 M₁ 没有邻接。因此，保持原样，将其读作 $\mathrm{(A \: + \: B \: + \: \bar{C})}$。
• 最大项 M₂ 只有一个邻接项 M₆。因此，将最大项 M₂ 展开为具有最大项 M₆ 的 2 平方，并将 2 平方读作 $\mathrm{(\bar{B} \: + \: C)}$。
• 最大项 M₄ 也只有一个邻接项 M₆。因此，将最大项 M₄ 展开为一个 2 平方数，其中最大项 M₆ 为 2 平方数，并将 2 平方数读作 $\mathrm{(\bar{A} \: + \: C)}$。
• 将所有求和项写成 POS 形式。

因此，简化的 POS 表达式为，

$$\mathrm{F \: = \: (A \: + \: B \: + \: \bar{C}) \: (\bar{B} \: + \: C) \: (\bar{A} \: + \: C)}$$

示例3

简化以下 SOP 形式的 4 变量布尔函数以获得最小 SOP 表达式。

$$\mathrm{F(A, \: B, \: C, \:D) \: = \: \sum \: m( 0,\: 1, \:3, \: 5, \: 7, \: 6, \: 10, \: 13, \: 14, \: 15)}$$

解决方案

给定布尔函数的 SOP K-map 表示如图 3 所示。

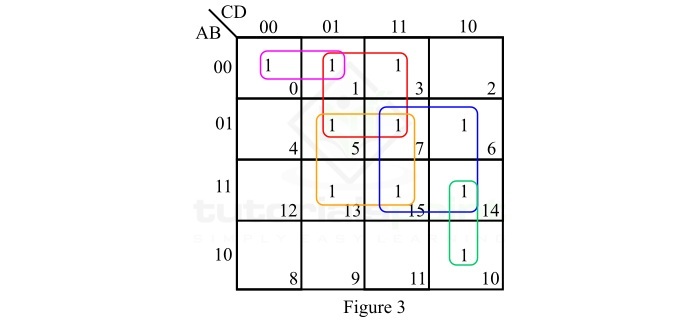
此 SOP K-map 的简化按照以下步骤进行 −

• 没有孤立的 1。
• 最小项 m₁ 有三个邻接项 m₃、m₅ 和 m₇。因此，将 m₁ 展开为具有最小项 m₃、m₅ 和 m₇ 的 4 方格，并将 4 方格读作 $\mathrm{\bar{A}D}$。
• 最小项 m5 有三个邻接项 m₇、m₁₃ 和 m₁₅。将 m₅ 展开为具有最小项 m₇、m₁₃ 和 m₁₅ 的 4 方格，并将 4 方格读作 BD。
• 最小项 m6 也有三个邻接项 m₇、m₁₄ 和 m₁₅。将 m6 展开为具有最小项 m₇、m₁₄ 和 m₁₅ 的 4 方格，并将 4 方格读作 BC。
• 最小项 m₁₀ 只有一个邻接项 m₁₄。将 m₁₀ 展开为具有最小项 m₁₄ 的 2 方格，并将 2 方格读作 $\mathrm{AC\bar{D}}$。
• 最小项 m₀ 也只有一个邻接项 m₁。将 m₀ 展开为一个具有最小项 m₁ 的 2 平方数，并将 2 平方数读为 $\mathrm{\bar{A}\bar{B}\bar{C}}$。
• 将所有乘积项写成 SOP 形式。

因此，简化的 SOP 表达式为，

$$\mathrm{F \: = \: \bar{A}D \: + \: BD \: + \: BC \: + \: AC\bar{D} \: + \: \bar{A}\bar{B}\bar{C}}$$

结论

这样，我们可以使用 K-map 简化给定的布尔表达式以获得最小表达式。尝试解决以下教程问题以更好地理解。

Q. 1 − 以 SOP 形式简化以下 3 变量布尔函数以获得其最小表达式。

$$\mathrm{F(A, \: B, \: C) \: = \: \sum \: m(1, \: 2, \: 4, \: 5, \: 7)}$$

Q. 2 −简化以下 SOP 形式的 4 变量布尔函数，以获得最小布尔表达式。

$$\mathrm{F(A, \: B, \: C, \: D) \: = \: \sum \: m(0, \: 1, \: 2, \: 4, \: 5, \: 7, \: 8, \: 9, \: 10, \: 12, \: 14, \: 15)}$$