数字电子中的全减法器
什么是全减法器?
全减法器是一个组合电路,有三个输入 A、B、bin 和两个输出 d 和 b。其中,A 为被减数,B 为减数,bin 为前一级产生的借位,d 为差输出,b 为借位输出。
众所周知,半减法器只能用于二进制数的 LSB(最低有效位)减法。如果在两个二进制数的 LSB 减法过程中出现借位,则会影响下一级的减法。因此,带借位的减法由全减法器执行。
图 1 显示了全减法器的框图和电路图。
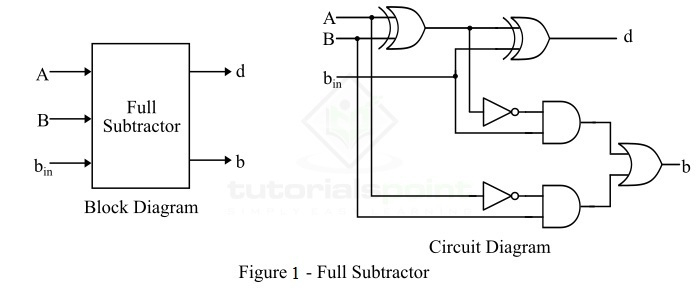
因此,我们可以使用两个 XOR 门、两个 NOT 门、两个 AND 门和一个 OR 门来实现全减法器。
全减法器的操作
现在,让我们了解全减法器的操作。全减器根据二进制减法规则执行操作以查找两个二进制数的差,如下所示 −
对于全减器,输出变量(差和借位)的 1 和 0 由 A – B – bin 的减法确定。
从全减器的逻辑电路图中可以清楚地看出,差位 (d) 是通过两个输入 A、B 和 bin 的 XOR 运算获得的,而输出借位 (b) 是通过变量 A、B 和 bin 的 NOT、AND 和 OR 运算获得的。
全减器的真值表
真值表是给出逻辑电路输入和输出之间关系的表。以下是全减法器的真值表 −
| 输入 | 输出 | |||
|---|---|---|---|---|
| A | B | Bin | D (Difference) | B (Borrow) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
全减法器的 K-Map
我们可以使用 K-Map(或卡诺图)这种简化布尔代数的方法来确定差分位(d)和输出借位(b)的方程。
半减法器的 K-Map 简化如图 2 所示。
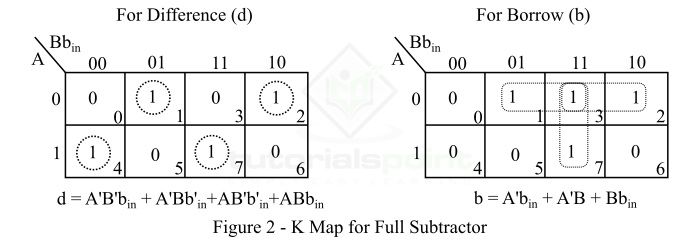
全减法器的特征方程
全减法器的特征方程,即差分(d)和借位输出(b)的方程,是通过遵循二进制减法规则获得的。这些方程如下所示 −
全减法器的差 (d) 是 A、B 和 bin 的异或。因此,
$$\mathrm{Difference, \: d \: = \: A \oplus B \oplus b_{in} \: = \: A'B'b_{in} \: + \: AB'b'_{in} \: + \: A'Bb'_{in} \: + \: ABb_{in}}$$
全减法器的借位 (b) 由以下公式给出:
从逻辑电路图和 k-map −
$$\mathrm{Borrow, \: b \: = \: A'B \: + \: \left ( A \oplus B \right ) \: 'b_{in}}$$
From Truth Table
$$\mathrm{Borrow, \: b \: = \: A'B'b_{in} \: + \: A'Bb'_{in} \: + \: A'Bb_{in} \: + \: ABb_{in}}$$
或者
$$\mathrm{Borrow, \: b \: = \: A'B \left ( b_{in} \: + \: b'_{in} \right ) \: + \: \left (AB \: + \: A'B' \right )b_{in} \: = \: A'B \: + \: \left (A \oplus B \right )'b_{in}}$$
全减法器的应用
以下是全减法器的一些重要应用 −
- 全减法器用于计算机 CPU 中的 ALU(算术逻辑单元)。
- 全减法器广泛用于在电子计算器和许多其他数字设备中执行减法等算术运算。
- 全减法器用于不同的微控制器进行算术减法。
- 它们用于计时器和程序计数器(PC)。
- 全减法器还用于处理器中以计算地址、表格等。
- 全减法器还用于 DSP(数字信号处理)和基于网络的系统。
结论
从以上讨论中,我们可以得出结论全减法器是一种组合逻辑电路,可以计算三个二进制数字的差值。在全减法器中,前一级的借位(如果有)也用于下一级的减法运算。因此,全减法器用于对任意位数的二进制数进行减法运算。


