数字电子器件中同步计数器的设计
在数字电子器件中,一组响应输入端施加的脉冲而改变其状态的触发器称为数字计数器。在数字计数器电路中,触发器的连接方式使得它们在任何时间的组合状态都是截至当时发生的总脉冲数的二进制等效值。因此,顾名思义,计数器用于在数字系统中计数脉冲。
数字计数器分为以下两种类型,即
- 异步计数器 −触发器以不同时触发的方式连接的计数器称为异步计数器。异步计数器也称为波纹计数器。
- 同步计数器 − 所有触发器同时计时的计数器称为同步计数器。
在了解了计数器的基础知识之后,现在让我们讨论同步计数器的设计。
同步计数器的设计
同步计数器是一种所有触发器都由同一时钟脉冲同时触发的计数器。设计同步计数器的系统过程如下所述。
步骤 1:确定所需触发器的数量
首先,分析问题描述并确定实现同步计数器所需的触发器数量。如果 n 是所需的触发器数量,那么 n 的最小值应使状态数 N 小于或等于 2n。
步骤 2:绘制状态图
其次,绘制显示所有可能状态的状态图。状态图基本上是一种图形方式,用于表示计数器进展的状态序列。在状态图中,我们还可以包括计数器在下一个时钟脉冲上从无效状态进入特定状态的情况。
步骤 3:选择触发器和激励表
在第三步中,选择用于实现计数器的特定类型的触发器并绘制其激励表。激励表提供有关触发器的当前状态、下一个状态和所需激励的信息。
步骤 4:获取激励的最小化表达式
现在,使用任何最小化技术(例如 K 图)获取触发器激励的最小表达式。
步骤 5:绘制逻辑图
最后,根据步骤 4 中获得的最小表达式绘制逻辑电路图。
这样,我们可以设计一个同步计数器
同步计数器可能存在锁定问题,这意味着它们可能无法自启动。自启动计数器是一种同步计数器,无论其初始状态如何,它都会进入其正确的状态序列。我们可以通过设计计数器使其在进入无效状态时进入特定状态,从而使其能够自启动。
现在,让我们举一个例子来了解设计同步计数器的过程。
示例
使用 D 触发器设计一个同步计数器,该计数器经历状态 0、1、2、4、0。未使用的状态在下一个时钟脉冲时必须始终变为零。
解决方案
此同步计数器按以下步骤设计 −
步骤 1 − 所需触发器数量 −
此同步计数器有四个稳定状态,即 0 (000)、1 (001)、2 (010)、4 (100)。但是我们需要三个触发器,因为它也计数 4(100)。因为三个触发器可以计数八个状态。因此,其余四个状态,即 3(011)、5(101)、6(110)和 7(111)是未使用的状态。根据问题陈述,未使用的状态必须在下一个时钟脉冲后变为 0(000)。因此,没有无关紧要的状态。
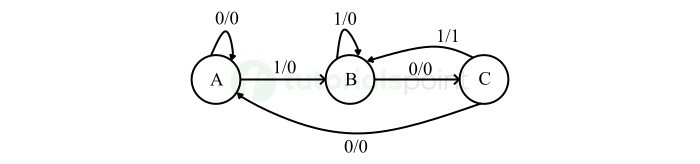
步骤 2 − 绘制状态图 −
0、1、2、4、0、… 计数器的状态图如下图所示绘制。
步骤 3 −选择触发器的类型并写出激励表 −
将使用 D 触发器,使用 D 触发器的计数器的激励表如下所示。
| 当前状态 | 下一个状态 | 所需激励 | ||||||
|---|---|---|---|---|---|---|---|---|
| Q3 | Q2 | Q1 | Q3 | Q2 | Q1 | D3 | D2 | D1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
步骤 4 − 导出最小表达式 −
从激励表中,我们可以看到没有最小化的可能。因此,激发的表达式可以直接从激发表本身写出,如下所示 −
$$\mathrm{D_{1}\:=\:Q_{3}^{'}Q_{2}^{'}Q_{1}^{'}}$$
$$\mathrm{D_{2}\:=\:Q_{3}^{'}Q_{2}^{'}Q_{1}^{'}}$$
$$\mathrm{D_{3}\:=\:Q_{3}^{'}Q_{2}^{'}Q_{1}^{'}}$$
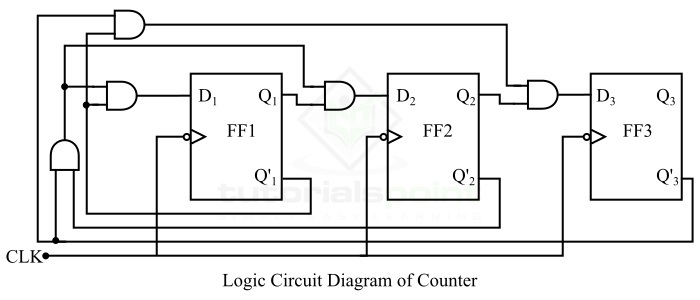
步骤 5 −绘制逻辑电路图 −
按照表达式,计数器 0、1、2、4、0、… 的逻辑电路图如下图所示。
这就是如何设计同步计数器的全部内容。


