数字电子技术 - 比较器
在数字电子技术中,比较器是一种组合逻辑电路,用于比较两个二进制数的大小。比较器用于多种不同的电子电路,如模拟数字转换器、电压电平检测器、过零检测器等。
比较器最基本的例子是 XNOR 门,只有当两个输入相等时,它才会产生高电平或逻辑 1 输出。
在本章中,我们将了解数字电子技术中比较器的基础知识、类型和应用。那么,让我们从比较器的基本定义开始。
什么是比较器?
用于比较两个二进制数的大小以确定相等或不相等的数字组合电路称为比较器。
因此,比较器的主要功能是比较输入数字的值并产生输出,指示数字是否相等或指定哪个数字更大。
让我们借助一个例子来了解比较器的工作原理。
考虑两个 3 位二进制数 A2A1A0 和 B2B1B0。如果这两个二进制数的所有对应位都一致,则称其相等。换句话说,如果 A2 = B2、A1 = B1 且 A0 = B0,则这两个二进制数相等。
下图显示了典型比较器的框图 −
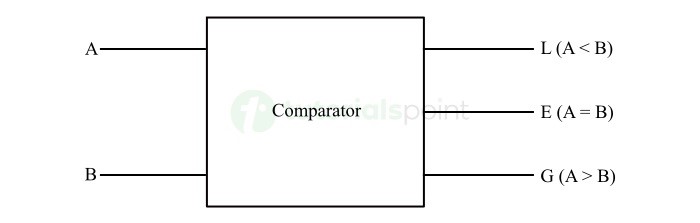
这里,A 和 B 是输入位,L、E 和 G 是输出线,其中 L 表示哪个数字较小,E 表示相等,G 表示数字较大。
比较器的类型
根据位数,以下是数字电路中使用的一些主要比较器类型 −
- 1 位幅度比较器
- 2 位幅度比较器
- 4 位幅度比较器
让我们详细讨论每种类型的比较器。
1 位幅度比较器
1 位幅度比较器 是一种逻辑电路,可以比较两个各为 1 位的二进制数。它产生的输出表示两个输入数字之间的关系。
换句话说,1 位幅度比较器是比较两个 1 位二进制数并产生输出以显示一个数字是否等于、大于或小于另一个数字的比较器。
1 位幅度比较器的框图如下图所示 −
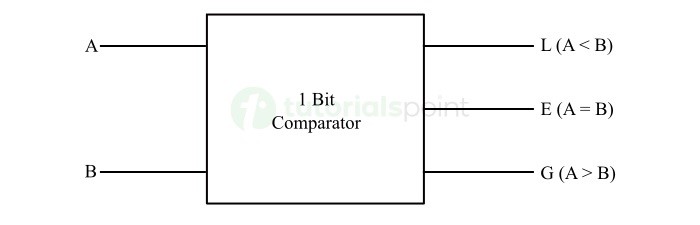
这里,A 和 B 是 1 位输入数字,L、E 和 G 是输出线,分别表示 A 和 B 之间小于、等于或大于的关系。
让我们了解这种比较器的工作原理。
如果 A = 0 且 B = 0 或者 A = 1 且 B = 1,则 A = B。它表示两个二进制数相等。因此,
$$\mathrm{E \: = \: \overline{A} \: \cdot \: \overline{B} \: + \: A \: \cdot \: B \: = \: A \: \odot \: B}$$
如果 A = 0 且 B = 1,则 A < B。这表示二进制数 A 小于二进制数 B。因此,
$$\mathrm{L \: = \: \overline{A} \: B}$$
如果 A = 1 且 B = 0,则 A > B. 它表示二进制数 A 大于二进制数 B。因此,
$$\mathrm{G \: = \: A \: \overline{B}}$$
1 位幅度比较器比较输入数 A 和 B 的相应位。为此,它使用不同类型的逻辑门。
1 位幅度比较器的真值表如下所示 −
| 输入 | 输出 | |||
|---|---|---|---|---|
| A | B | L (A < B) | E (A = B) | G (A > B) |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 |
我们可以利用该真值表得到1位幅度比较器的布尔表达式。
$$\mathrm{L \: = \: \overline{A} \: B}$$
$$\mathrm{E \: = \: \overline{A} \: \cdot \: \overline{B} \: + \: A \: \cdot \: B \: = \: A \: \odot \: B}$$
$$\mathrm{G \: = \: A \: \overline{B}}$$
1位幅度比较器的逻辑电路图如下图所示。
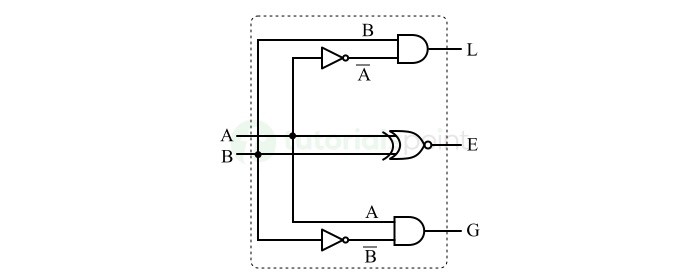
它由两个与门、两个非门和一个异或门组成。
2位幅度比较器
用于比较两个2位二进制数的幅度并确定它们之间关系的数字组合电路称为2位幅度比较器。
因此,2位幅度比较器比较两个2位二进制数所表示的值,然后生成一个输出,指示一个数字是等于、大于还是小于另一个数字。
典型电路的框图2 位幅度比较器如下图所示 −
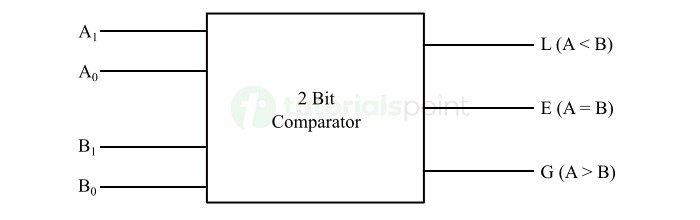
此处,线 A0A1 和 B0B1 表示两个 2 位二进制数输入,线 L、E 和 G 表示小于、等于和大于输出线。
我们可以借助下面给出的真值表理解 2 位幅度比较器的操作 −
| 输入 | 输出 | |||||
|---|---|---|---|---|---|---|
| A1 | A0 | B1 | B0 | L (A < B) | E (A = B) | G (A > B) |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 |
现在让我们推导出输出 L、E 和 G 的布尔表达式。
情况 1:A = B
如果 A0 = B0 且 A1 = B1,则比较器产生输出 A = B,即 E。因此,输出 E 的布尔表达式为,
$$\mathrm{E \: = \: (A_{0} \: \odot \: B_{0}) \: (A_{1} \: \odot \: B_{1})}$$
情况 2:A < B
比较器产生输出 A < B 是 L,若
- A1 = 0 且 B1 = 1,或
- A1 = B1 且 A0 = 0 且 B0 = 1。
从这些语句,我们可以为输出 L 写出布尔表达式如下 −
$$\mathrm{L \: = \: \overline{A_{1}} \: B_{1} \: + \: (A_{1} \: \odot \: B_{1}) \: \overline{A_{0}} \: B_{0}}$$
情况 3:A > B
比较器的输出将是 A > B 即 G,如果
- A1 = 1 且 B1 = 0,或
- A1 = B1 且 A0 = 1 且 B0 = 0。
从这些语句中,输出 G 的布尔表达式将是,
$$\mathrm{G \: = \: A_{1} \: \overline{B_{1}} \: + \: (A_{1} \: \odot \: B_{1}) \: A_{0} \: \overline{B_{0}}}$$
下图显示了 2 位幅度比较器的逻辑电路图 −

4 位幅度比较器
4 位幅度比较器用于更复杂的数字电路,如微处理器、微控制器等。
它是一种比较器,可以比较两个 4 位二进制数的值或幅度,并产生一个输出,指示一个数字是等于、小于还是大于另一个数字。
下图显示了 4 位幅度比较器的框图 −
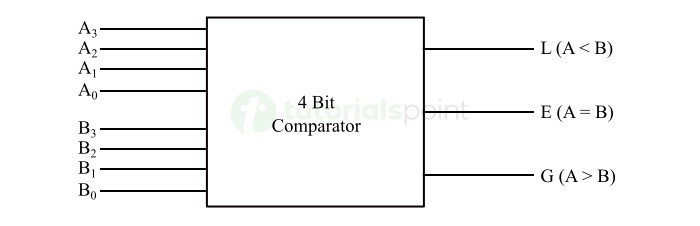
现在让我们了解一下这个 4 位幅度比较器的工作原理。为此,考虑 A = A3A2A1A0 是第一个 4 位二进制数,B = B3B2B1B0 是第二个 4 位二进制数。
比较器将显示以下结果 −
情况 1:A = B
如果两个数字的所有对应位都相等,即 A3 = B3 且 A2 = B2 且 A1 = B1 且 A0 = B0,则比较器将产生输出 A = B,即 E。
在这种情况下,输出的布尔表达式将是,
$$\mathrm{E \: = \: (A_{3} \: \odot \: B_{3}) \: (A_{2} \: \odot \: B_{2}) \: (A_{1} \: \odot \: B_{1}) \: (A_{0} \: \odot \: B_{0})}$$
情况 2:A < B
比较器将产生输出 A < B 为 L,如果
- A3 = 0 且 B3 = 1,或
- A3 = B3 且如果 A2 = 0 且 B2 = 1,或
- A3 = B3 且如果 A2 = B2 且如果 A1 = 0 且 B1 = 1,或
- A3 = B3 且如果 A2 = B2 且如果 A1 = B1 且如果 A0 = 0 且B0 = 1。
从这些语句中,我们可以得出输出 L 的布尔表达式,如下所示。
$$\mathrm{L \: = \: \overline{A_{3}} \: B_{3} \: + \: (A_{3} \: \odot \: B_{3}) \: \overline{A_{2}} \: B_{2} \: + \: (A_{3} \: \odot \: B_{3}) \: (A_{2} \: \odot \: B_{2}) \: \overline{A_{1}} \: B_{1} \: + \: (A_{3} \: \odot \: B_{3}) \: (A_{2} \: \odot \: B_{2}) \: (A_{1} \: \odot \: B_{1}) \: \overline{A_{0}} \: B_{0}}$$
情况 3:A > B
比较器产生输出 A > B 是 G,如果
- A3 = 1 且 B3 = 0,或
- A3 = B3 且如果 A2 = 1 且 B2 = 0,或
- A3 = B3 且如果 A2 = B2 且如果 A1 = 1 且 B1 = 0,或
- A3 = B3 且如果 A2 = B2 且如果 A1 = B1 且如果 A0 = 1 且B0 = 0。
因此,从这些语句中,我们可以为输出 G 写出布尔表达式,即
$$\mathrm{G \: = \: A_{3} \: \overline{B_{3}} \: + \: (A_{3} \: \odot \: B_{3}) \: A_{2} \: \overline{B_{2}} \: + \: (A_{3} \: \odot \: B_{3}) \: (A_{2} \: \odot \: B_{2}) \: A_{1} \: \overline{B_{1}} \: + \: (A_{3} \: \odot \: B_{3}) \: (A_{2} \: \odot \: B_{2}) \: (A_{1} \: \odot \: B_{1}) \: A_{0} \: \overline{B_{0}}}$$
4位幅度比较器的逻辑电路实现如下图所示 −
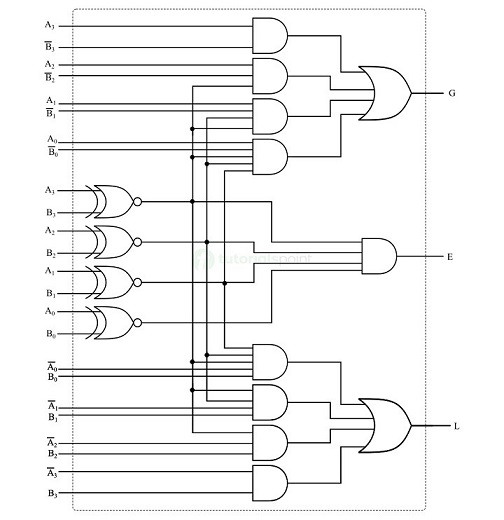
比较器 IC
比较器 IC 是一种集成电路,用于比较两个二进制数并根据比较结果产生输出。
常用的比较器 IC 是 IC 7485,它是一种 4 位幅度比较器 IC。在数字电子应用中,它广泛用于比较两个 4 位二进制数。
IC 7485 比较两个输入数字的相应位,并确定一个数字是否等于、大于或小于另一个数字。下图为 IC 7485 的引脚图。
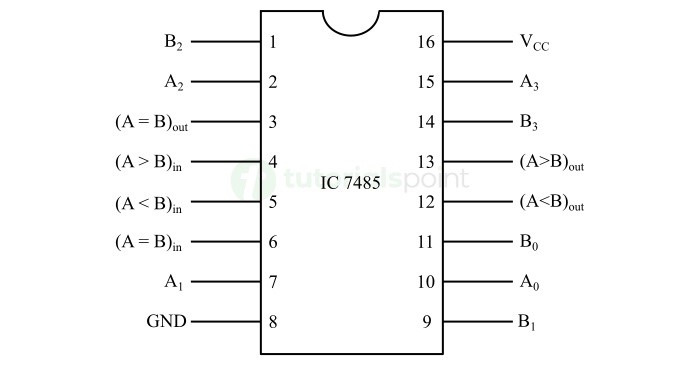
该 IC 广泛应用于各种数字电路,如微处理器、微控制器、控制系统和算术逻辑单元。
比较器的应用
比较器是各种数字电路中的基本组件。它们提供比较电压电平和做出决策的功能。
下面列出了比较器在数字电子领域的一些关键应用 −
- 比较器用于检测电子电路中电压电平的变化。
- 比较器也用于温度监测系统。
- 比较器用作各种电源电路中的过零检测器,如相位控制电路、电机和电源控制电路等。
- 比较器是模数转换器 (ADC) 中的关键组件。
- 在信号调节电路中,比较器用于在处理之前放大和过滤信号。
结论
总之,比较器是一种组合逻辑电路,用于各种数字电子应用中,以比较两个相似的量,如两个 2 位二进制数或两个电压电平等。
比较器帮助我们根据两个输入的比较做出决策值。它们广泛用于多种不同的电子设备和系统,例如算术逻辑单元、基于微处理器的系统、控制系统、自动化系统和电信系统。
根据特定应用所需的输入位数,我们可以设计 1 位、2 位或 4 位比较器。此外,比较器以集成电路的形式提供。最常用的 IC 比较器是 IC 7485,它是一个 4 位幅度比较器。


