数字电子技术 - 二进制算术
二进制算术是数字电子技术和计算机工程领域的基本概念之一。它基本上是二进制数的数学,允许对二进制数执行各种算术运算。我们知道二进制数字系统有两个数字,即 0 和 1,用于表示数字系统的开启或关闭状态。因此,二进制算术构成了数字计算的基础。
在本章中,我们将讨论以下四个主要的二进制算术运算−
- 二进制加法
- 二进制减法
- 二进制乘法
- 二进制除法
让我们详细讨论这些二进制算术运算以及解决的示例。
二进制加法
在二进制算术中,将两个二进制数相加的过程称为二进制加法。其中,二进制数仅由 0 和 1 组成。在二进制加法中,当和大于 1 时会产生进位。
二进制加法规则
两个二进制数的加法按照这些二进制算术规则执行 −
$$\mathrm{0 \: + \: 0 \: = \: 0}$$
$$\mathrm{0 \: + \: 1 \: = \: 1}$$
$$\mathrm{1 \: + \: 0 \: = \: 1}$$
$$\mathrm{1 \: + \: 1 \: = \: 10 \: (Sum \: = \: 0 \:\ \& \: 进位 \: = \: 1)}$$
让我们考虑一些例子来理解二进制加法。
示例 1
将两个二进制数 1101 和 1110 相加。
解决方案
给定二进制数的二进制加法如下 −
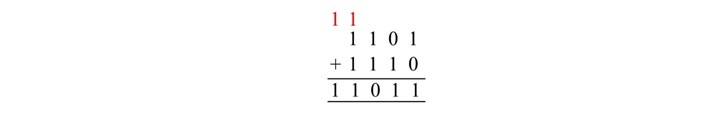
解释
将 1(第一个数字的最右边的位)和 0(第二个数字的最右边的位)相加。结果为 1 + 0 = 1(因此,将 1 记为和位)。
将 0(第一个数字的第二个最右边的位)和 1(第二个数字的第二个最右边的位)相加。结果是 0 + 1 = 1(记为和位)。
将 1(第一个数字的第三个最右边位)和 1(第二个数字的第三个最右边位)相加。结果是 1 + 1 = 10(记为和,记为 0,记为进位)。
将 1(第一个数字的最左边位)、1(第二个数字的最左边位)和 1(进位)相加。结果是 1 + 1 + 1 = 11(记为和,记为 1,记为进位)。
在和的进位 1 周围写上结尾。
因此,结果是 11011。
示例 2
将 1010 和 11011 相加。
解决方案
下面解释了给定数字的二进制加法 −

解释
将 0(第一个数字的最右边位)和 1(第二个数字的最右边位)相加。结果为 0 + 1 = 1(将 1 记为和)。
将 1(第一个数字的第二右位)和 1(第二个数字的第二右位)相加。结果为 1 + 1 = 10(将 0 记为和,将 1 记为进位)。
将 0(第一个数字的第三右位)、0(第二个数字的第三右位)和 1(进位)相加。结果为 0 + 0 + 1 = 1(将 1 记为和)。
将 1(第一个数字的最左边位)和 1(第二个数字的第二左位)相加。结果是 1 + 1 = 10(记 0 作为和,1 作为进位)。
添加 1(第二个数字的最左边的位)和 1 个进位。它给出 1 + 1 = 10(将 0 记为和,将 1 记为进位末尾)。
因此,1010 和 11011 的总和为 100101。
二进制减法
在二进制算术中,二进制减法是一种数学运算,用于查找两个二进制数之间的差异。
在二进制减法中,从最右边的位开始,减去二进制数的每一位。
此外,如果需要,可以从更高的位中取出借位。
二进制减法规则
二进制减法按照以下二进制算术规则执行 −
$$\mathrm{0 \: – \: 0 \: = \: 0}$$
$$\mathrm{1 \: – \: 0 \: = \: 1}$$
$$\mathrm{0 \: – \: 1 \: = \: 1 \: (borrow \: 1 \: from \: the \: next \: higher \: bit)}$$
$$\mathrm{1 \: – \: 1 \: = \: 0}$$
让我们看一些例子来理解二进制减法。
示例 1
从 1101 中减去 1100。
解决方案
给定二进制数的减法如下所示−
1101 – 1100 = 0001
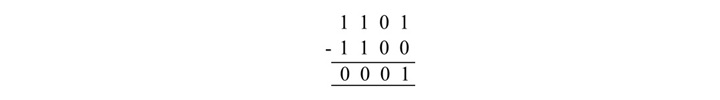
解释
从 1(第一个数字的最右边位)中减去 0(第二个数字的最右边位)。结果为 1 – 0 = 1(记 1 作为差值)。
从 0(第一个数字的最右边第二位)中减去 0(第二个数字的最右边第二位)。结果为 0 – 0 = 0。
从 1(第一个数字的最右边第三位)中减去 1(第二个数字的最右边第三位)。结果为 1 – 1 = 0。
从 1(第一个数字的最左边位)中减去 1(第二个数字的最左边位)。结果为 1 – 1 = 0。
因此,1101 和 1100 的差为 0001。
示例 2
从 1111 中减去 101。
解决方案
下面解释给定二进制数的减法 −
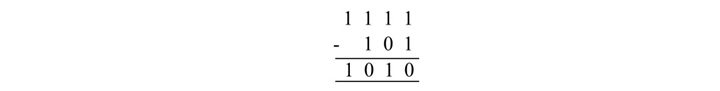
解释
减去最右边的位:1 – 1 = 0
减去第二个最右边的位:1 – 1 = 1
减去第三个最右边的位:1 – 1 = 0
减去最左边的位:1 – 0 = 1
因此,结果为 1010。
示例 3
从 1101 中减去 1011。
解决方案
1101 和 1011 的二进制减法如下所示 −

解释
减去最右边的位:1 – 1 = 0。
减去第二个最右边的位:0 – 1 = 1。从下一个更高的位借位 1。
减去第三个最右边的位:0 – 0 = 0。1 借位给予前一位。
减去最左边的位:1 – 1 = 0。
因此,1101 和 1011 的差是 0010。
二进制乘法
在二进制算术中,二进制乘法是将两个二进制数相乘并得到它们的乘积的过程。
在二进制乘法,我们将一个二进制数的每一位与另一个二进制数的每一位相乘,然后将部分乘积相加得到最终乘积。
二进制乘法规则
两个二进制数的乘法按照以下二进制算术规则执行 −
$$\mathrm{0 \: imes \: 0 \: = \: 0}$$
$$\mathrm{0 \: imes \: 1 \: = \: 0}$$
$$\mathrm{1 \: imes \: 0 \: = \: 0}$$
$$\mathrm{1 \: imes \: 1 \: = \: 1}$$
很明显,二进制乘法与十进制乘法相似。让我们借助已解决的示例来理解二进制乘法。
示例 1
将 1101 乘以 11。
解决方案
下面描述了给定数字的二进制乘法 −

解释
将第二个数字的最右边位 1 乘以第一个数字 (1101) 的每个位。
现在,将部分乘积向左移动一位以执行下一个乘法。
将第二个数字的最左边位 1 乘以第一个数字 (1101) 的每个位。
最后,将所有部分乘积相加以获得最终乘积。
因此,1101 和 11 的乘积为 100111。
示例 2
将 11011 和 110 相乘。
解决方案
给定二进制数的乘法如下所示 −
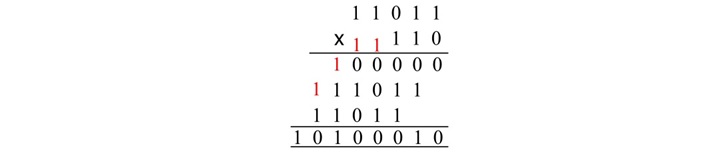
解释
将第二个数的最右位 (0) 与第一个二进制数 (11011) 的每个位相乘。
将部分积向左移动一位。
将第二个数的第二右位 (1) 与第一个二进制数 (11011) 的每个位相乘。
再次将部分积向左移动一位。
将第二个数的最左位 (1) 与第一个数的每个位相乘。
然后,将所有部分积相加以获得最终结果乘积。
因此,11011 和 110 的乘积是 10100010。
二进制除法
二进制除法是用于在将一个二进制数除以另一个二进制数时求出商和余数的基本算术运算之一。
二进制除法规则
在将一个二进制数除以另一个二进制数时,会运用以下二进制算术规则 −
$$\mathrm{0 \: \div \: 0 \: = \: Undefined}$$
$$\mathrm{0 \: \div \: 1 \: = \: 0 \: with \: Remainder \: = \: 0}$$
$$\mathrm{1 \: \div \: 0 \: = \: Undefined}$$
$$\mathrm{1 \: \div \: 1 \: = \: 1 \: with \: Remainder \: = \: 0}$$
二进制除法程序
- 从被除数的最左边的位开始除以除数。
- 将除数得到的商乘以被除数并从被除数中减去。
- 将被除数的下一位降低并重复除法过程,直到使用给定被除数的所有位。
让我们考虑一些已解决的示例以了解二进制除法。
示例 1
将 110011 除以 11。
解决方案
给定二进制数的除法解释如下 −
110011 ÷ 11 = 10001
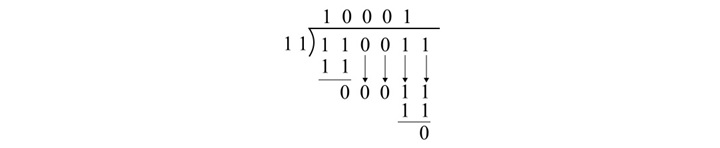
在此二进制除法示例中,所得商为 10001,余数为 0。
示例 2
将 11011 除以 10。
解决方案
以下解释 11011 除以 10 的二进制除法 −
11011 ÷ 10 = 1101
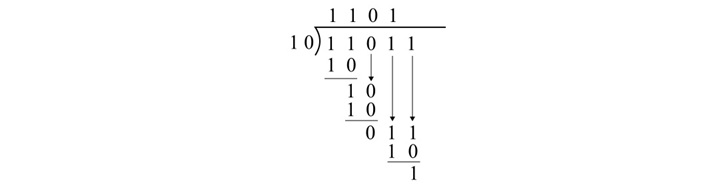
在此示例中,商为 1101,余数为 1。
结论
二进制算术涉及对二进制数执行的算术运算。一般来说,二进制数有四种基本算术运算,即加法、减法、乘法和除法。
在本章中,我们解释了执行所有四种基本二进制算术运算的规则和程序,并给出了解决的示例。


