数字电子技术 - 有限状态机
有限状态机是各种数字和计算系统的基本构建块。它们提供了一种系统的方法来模拟顺序电路的行为。它们还有助于控制数字系统中的各种过程。
阅读本章以了解有限状态机的组件、类型、优势和应用。
什么是有限状态机?
有限状态机 (FSM) 是一种数学模型,用于解释和理解数字系统的行为。更具体地说,它是一个结构化和系统的模型,有助于理解在给定时间点存在于有限数量状态中的顺序电路的行为。
更简单地说,如果同步顺序电路具有有限数量的状态,则也称为有限状态机 FSM。
这些有限状态的转换基于内部或外部输入,从而导致系统行为发生可预测和系统性的变化。
有限状态机的组件
典型的有限状态机由以下主要组件组成 −
有限状态
有限状态不过是给定系统中的不同模式或条件。这些有限状态中的每一个都代表特定的行为。在数字系统表示中,这些有限状态通常通过符号或标签表示。
状态转换
就有限状态机而言,状态转换可以定义为从一种状态到另一种状态的变化。这种状态变化或状态转换是基于某些特定输入或条件而发生的。这些状态转换通常由与某些规则或条件相关的事件触发,并确定系统的下一个状态。
状态图
有限状态机的状态转换和行为可以用图形形式表示,称为有限状态机的状态图。
输入
有限状态机的输入是触发系统状态转换的外部信号。这些输入将通过使用传感器、用户输入设备(如麦克风、键盘等)输入到有限状态机中。
输出
系统根据输入和当前状态产生的结果称为输出。系统的这些输出可用于触发事件、控制执行器或向外部环境提供反馈。
有限状态机的类型
有限状态机有两种类型,即
- Mealy 状态机
- Moore 状态机
现在让我们详细讨论这两种类型的有限状态机。
Mealy 状态机
如果有限状态机的输出取决于当前输入和当前状态,则称其为 Mealy 状态机。Mealy 状态机的框图如下图所示 −
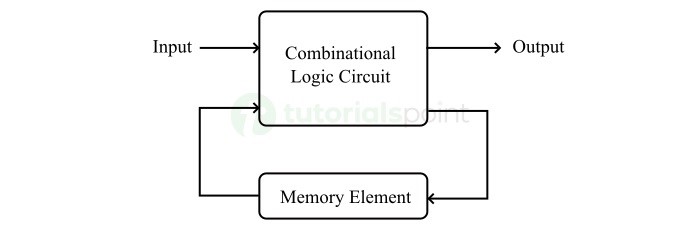
如图所示,Mealy 状态机有两个主要部分。它们是组合逻辑电路和存储元件。存储元件可用于将先前输出和当前状态的一部分作为输入提供给组合逻辑电路。
基于当前输入和当前状态,Mealy 状态机产生输出。因此,输出仅在时钟信号的正或负转换时有效。
Mealy状态机的状态图
Mealy状态机的状态图如下图所示。
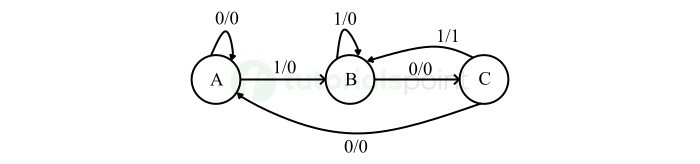
在上图中,有三个状态,分别是A,B和C。这些状态在圆圈内标记,每个圆圈对应一个状态。这些状态之间的状态转换用有向线表示。这里,0 / 0,1 / 0和1 / 1表示输入/输出。在上图中,根据输入的值,每个状态有两个状态转换。
通常,Mealy状态机所需的状态数小于或等于Moore状态机所需的状态数。每个 Mealy 状态机都有一个等效的 Moore 状态机。
Moore 状态机
如果有限状态机的输出仅取决于当前状态,则称其为 Moore 状态机。
Moore 状态机的框图如下图所示 −
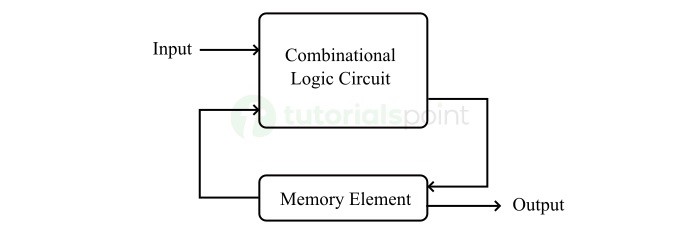
如上图所示,Moore 状态机有两个部分。即组合逻辑和内存。在这种情况下,当前输入和当前状态决定下一个状态。因此,基于下一个状态,Moore 状态机产生输出。因此,只有在状态转换后,输出才会有效。
Moore 状态机的状态图
Moore 状态机的状态图如下图所示 −
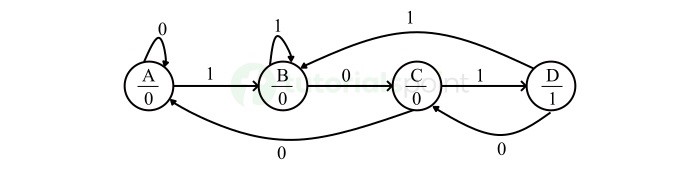
上图中,有四个状态,即 A、B、C 和 D。这些状态和相应的输出都标记在圆圈内。这里,每个转换只标记输入值。在上图中,根据输入值,每个状态都有两个转换。
通常,Moore 状态机所需的状态数大于或等于 Mealy 状态机所需的状态数。每个 Moore 状态机都有一个等效的 Mealy 状态机。因此,我们可以根据需求使用其中一种。
有限状态机的优势
有限状态机在数字电子领域具有多种优势。所有这些优势使它们成为建模和实现各种数字系统的重要工具。有限状态机的一些关键优势如下所列 −
- 有限状态机提供了一种简单而系统的方法来建模和理解具有离散有限状态及其之间转换的数字系统的行为。
- 有限状态机支持模块化设计,有助于将复杂的数字系统分解为更小的组件。有限状态机的每个组件都可以代表整个系统的特定任务。这使得设计、测试和维护更加容易。
- 有限状态机在可扩展性方面提供了便利,允许在不改变其基本结构或操作的情况下向现有系统添加新的状态和转换以及逻辑。当系统需求发展或扩展时,这一点变得至关重要。
- 从根本上讲,有限状态机具有确定性或可预测的行为。这意味着,我们可以轻松地根据系统的当前状态和输入确定系统的下一个状态。这种可预测的行为有助于我们确保系统的可靠和一致运行。这也使得有限状态机最适合实时和安全关键型应用。
- 有限状态机在硬件和软件实现方面都被认为是高效的,因为它们需要最少的硬件和软件资源,例如逻辑门、内存和其他处理资源。
- 有限状态机支持并行性。该技术允许在系统内同时发生多个状态和状态转换。它还优化了性能并提高了系统的响应能力。
- 有限状态机是数字电子和计算机科学领域的多功能工具,因为它们在数字系统设计、控制系统设计、软件开发、人工智能开发等各个领域都有应用。
有限状态机的应用
在数字电子和计算机科学领域,有限状态机因其能够有效地建模顺序逻辑系统而被用于各种应用中。以下是有限状态机应用的一些示例 −
- 有限状态机通常用于设计和实现不同类型的顺序逻辑电路,例如数字计数器、计时器、控制单元等。
- 有限状态机用于数字控制系统,以控制和调节复杂自动化系统的行为,如机器人、工业控制和自动化系统等。
- 有限状态机用于实现通信协议(如网络协议)和基于状态的数字系统(如数据传输和协议转换器)。
- 有限状态机还用于软件开发领域,以建模和定义应用程序中基于状态的系统的行为,创建用户界面,实现游戏机制以及开发工作流管理系统。
结论
总之,有限状态机是数字电子领域用于建模、设计和分析行为的重要而强大的工具基于状态的数字系统和同步时序电路。
有限状态机允许工程师和系统设计人员设计和实现高效、可靠且可扩展的系统,以处理数字电子和计算机工程领域中复杂的基于状态的逻辑和流程。


