使用 NAND 门的半减法器
在数字电子技术中,减法器是一种组合逻辑电路,用于执行两个二进制数的减法。但是,二进制数的减法可以使用加法器电路通过取 1 或 2 的补码来执行。但是,我们也可以实现一个专用电路来执行两个二进制数的减法。
在两个二进制数的减法中,数字的每个减数位都从其对应的有效被减数位中减去以形成差位。在减法过程中,如果被减数位小于减数位,则从下一个位置借用 1。根据输入的位数,减法器有两种类型,即半减法器和全减法器。
半减法器以两个二进制数字为输入,输出一个差位和一个借位(如果有)。
另一方面,全减法器以三个位为输入,即两个是输入位,一个是来自前一级的输入借位,输出一个差位和一个输出借位。
由于减法器是组合逻辑电路,即由逻辑门组成。我们可以使用不同类型的逻辑门(如 AND、OR、NOT、NAND、NOR 等)来实现全加器电路。
在这里,我们将讨论使用 NAND 门实现半减法器。但在此之前,让我们先了解一下半减法器的基础知识。
什么是半减法器?
半减法器是一种组合电路,具有两个输入和两个输出,其中一个输出为差值,另一个输出为借位。半减法器产生输入端两个二进制位之间的差值,并产生借位输出(如果有)。在减法(A-B)中,A 称为被减数位,B 称为减数位。半减法器的框图如图 1 所示。
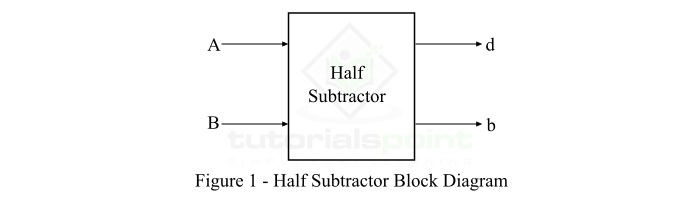
这里,A 和 B 是输入变量(二进制数字),d 是输出差位,b 是借位。我们可以借助真值表来理解半减法器的运行。
半减法器的真值表
以下是半减法器的真值表 −
| 输入 | 输出 | ||
|---|---|---|---|
| A | B | D (Difference) | B (Borrow) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
利用这个真值表,我们可以确定半减法器的输出方程。以下是差位 (d) 和借位 (b) 的等式 −
差位 (D) −
$$\mathrm{差,\: d \: = \: A'B \: + \: AB' \: = \: A \oplus B}$$
借位 (B)
$$\mathrm{借,\: b \: = \: A'B}$$
现在,让我们讨论使用 NAND 门实现半减法器。
使用 NAND 门的半减法器
我们可以实现半减法器的逻辑电路仅使用 NAND 门的减法器如图 2 所示。

从该逻辑电路图中,我们可以看到实现半减法器需要 9 个 NAND 门。
NAND 逻辑中半减法器的输出方程如下 −
Difference Bit (D)
$$\mathrm{Difference, \: d \: = \: \overline{\overline{A \cdot \: \overline{AB}} \: \cdot \: \overline{B \cdot \overline{AB}}} \ = \: A \oplus B}$$
Borrow Bit (B)
$$\mathrm{Borrow, \: b \: = \: \overline{\overline{B \cdot \: \overline{AB}}} \: = \: \overline{A} \: B}$$
这样,我们就可以仅使用 NAND 门来实现半减法器。


