数字电子技术中的 3 变量 K-Map

K-Map 或 卡诺图 是一种图形方法，用于简化布尔函数中的复杂代数表达式。此方法避免使用复杂的定理和方程式操作。K-Map 基本上是真值表的一种特殊形式，可以轻松映射出参数的值并给出简化的布尔表达式。

K-Map 方法最适合具有两到四个变量的布尔函数。但是，它也可以用于具有五或六个变量的布尔函数，但随着函数中变量数量的增加，其过程变得更加困难。

因此，在实践中，我们主要使用二变量 K-Map、三变量 K-Map 和四变量 K-Map。但有时，五变量 K-Map 和六变量 K-Map 也用于导出布尔表达式。

在这里，我们将讨论 3 变量 K-Map 及其在简化复杂布尔函数中的应用。

三变量 K-Map

我们可以使用 K-Map 来简化三变量的布尔函数。三个变量(A、B、C)的布尔函数可以用标准乘积和 (SOP) 形式表示，总共有八种可能的组合，如下所示 −

$$\mathrm{(A'B'C'), (A'B'C), (A'BC'), (A'BC), (AB'C'), (AB'C), (ABC'), (ABC)}$$

我们可以分别用 m₀、m₁、m₂、m₃、m₄、m₅、m₆ 和 m₇ 来表示这些组合中的每一个。这些项中的每一个都称为 最小项。在这些组合中，A称为MSB(最高有效位)，C称为LSB(最低有效位)。

以POS(和的乘积)形式表示，三个变量布尔表达式的八种可能组合如下 −

$$\mathrm{(A+B+C), (A+B+C'), (A+B'+C), (A+B'+C'), (A'+B+C), (A'+B+C'), (A'+B'+C), (A'+B'+C')}$$

这些组合中的每一个通常由M₀、M₁、M₂、M₃、M₄、M₅、M₆和M₇。这些项中的每一个都称为最大项。与最小项类似，A 称为 MSB(最高有效位)，C 称为 LSB(最低有效位)。

因此，三变量 K-Map 有八个(2³)方块或单元格，K-Map 上的每个方块代表最大项的最小项，如下图所示。

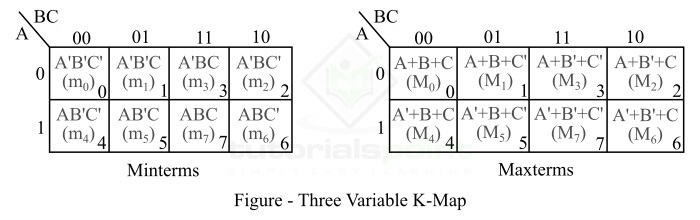
这里，每个单元格右下角的小数字表示最小项或最大项的名称。

K-Map 顶部的二进制数表示每列变量 B 和 C 的条件。图左侧每行对应的二进制数表示该行变量 A 的条件。

例如，上图第四列顶部的二进制数 10 表示变量 B 以非补码形式出现，变量 C 以补码形式出现在该列的所有最小项中。K 图第一行左侧的二进制数 0 表示变量 A 以补码形式出现在所有最小项中，K 图第二行左侧的二进制数 1 表示变量 A 以非补码形式出现在所有最小项中。

另外，请注意，K 图顶部的二进制数不是按正常二进制顺序排列的，而是按格雷码排列的。 K-map 中使用格雷码可确保两个物理相邻的单元格实际上相邻，这意味着它们的最小项或最大项仅相差一个变量。

数值示例

在 K-Map 上映射以下三变量布尔表达式。

$$\mathrm{f \: = \: \overline{A} \: \overline{B} \: C \: + \: A \: \overline{B} \: C \: + \: \overline{A} \: B \: \overline{C} \: + \: A \: \overline{B} \: \overline{C} \: + \: A \: B \: C}$$

解决方案

在给定的布尔表达式中，最小项为 −

$$\mathrm{\overline{A} \: \overline{B} \: C \: = \: 001; \: A \: \overline{B} \: C \: = \: 101; \: \overline{A} \: B \: \overline{C} \: = \: 010; \: A \: \overline{B} \: \overline{C} \: = \: 100; \: ABC \: = \: 111}$$

因此，

$$\mathrm{m_{1} \: = \: \overline{A} \: \overline{B} \: C \: = \: 001}$$

$$\mathrm{m_{5} \: = \: A \: \overline{B} \: C \: = \: 101}$$

$$\mathrm{m_{2} \: = \: \overline{A} \: B \: \overline{C} \: = \: 010}$$

$$\mathrm{m_{4} \: = \: A \: \overline{B} \: \overline{C} \: = \: 100}$$

$$\mathrm{m_{7} \: = \: ABC \: = \: 111}$$

因此，表达式为:

$$\mathrm{f \: = \: \sum \: m (1, \: 5, \: 2, \: 4, \: 7)}$$

该表达式的 K 图如下图所示 −

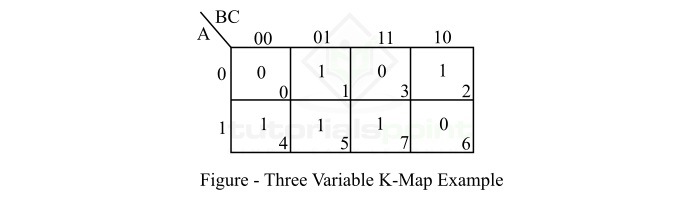
结论

从以上讨论中，我们可以得出结论，三变量 K 图是一种用于简化复杂三变量布尔函数的图形方法。三变量 K 图有八个方块或单元格。