NumPy - Zipf 分布
什么是 Zipf 分布?
Zipf 分布是一种离散概率分布,用于描述按降序排列的元素的频率。
它遵循元素的频率与其在频率表中的排名成反比的原则,这在自然语言中很常见,其中最常用的单词出现的频率是第二常用单词的两倍,是第三常用单词的三倍,依此类推。
它由参数"s"定义,该参数决定了分布的偏度。示例:大型文本语料库中的词频分布通常遵循 Zipf 分布。从数学上讲,Zipf 分布的概率质量函数 (PMF) 如下:
P(X = k) = (1 / ks) / H(N, s)
其中,k 是秩,s 是表征分布的指数,H(N, s) 是第 N 个广义调和数,用于对分布进行正则化。
在 NumPy 中生成 Zipf 样本
NumPy 提供了 numpy.random.zipf() 函数,用于根据 Zipf 分布生成随机样本。此函数需要两个主要参数:
- a: 分布参数,也称为指数。
- size: 要生成的样本数量(可选)。
示例:生成 Zipf 样本
以下示例从指数为 2 的 Zipf 分布中生成 10 个随机样本 -
import numpy as np
# 生成 Zipf 样本
a = 2
samples = np.random.zipf(a, size=10)
print("生成的 Zipf 样本:", sample)
以下是获得的输出 -
生成的 Zipf 样本:[1 3 1 2 1 1 1 1 2 1]
齐普夫分布的性质
齐普夫分布具有几个独特的性质,使其可用于建模现实世界的现象,它们是:-
- 厚尾:该分布具有厚尾,这意味着少数事件非常常见,而大多数事件则很少见。
- 幂律:事件发生的概率与其秩的指数次方成反比。
- 尺度不变:当测量尺度发生变化时,分布保持不变。
示例:可视化齐普夫定律
让我们将齐普夫分布可视化,以更好地理解其性质。我们可以使用 Matplotlib 绘制每个等级的出现频率 -
import numpy as np
import matplotlib.pyplot as plt
# 生成大量样本
a = 2
samples = np.random.zipf(a, size=1000)
# 统计每个等级的出现次数
unique, counts = np.unique(samples, return_counts=True)
# 绘制等级-频率分布
plt.figure(figsize=(10, 6))
plt.loglog(unique, counts, marker="o")
plt.title("Zipf 分布")
plt.xlabel("等级")
plt.ylabel("频率")
plt.show()
我们得到了一个对数-对数图,显示了每个等级的频率,展示 Zipf 分布的厚尾和幂律特性 -
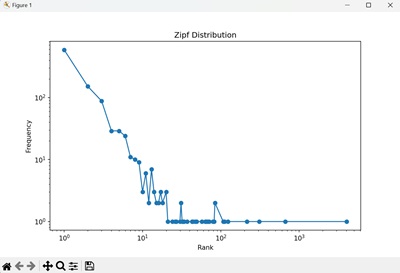
Zipf 分布的应用
Zipf 分布在各个领域都有应用,用于模拟少数事物非常常见而许多事物很少见的现象。常见应用包括 -
- 自然语言处理 (NLP): 在语料库中建模词频。
- 人口研究: 分析城市人口和规模。
- 互联网流量: 了解网页访问量和点击量的分布。
示例:文本中的词频
假设我们有一个文本文档,并希望使用 Zipf 分布对词频进行建模 -
import matplotlib.pyplot as plt
from collections import Counter
# 示例文本
text = "the quick brown fox jumps over the lazy dog the quick brown fox"
# 将文本拆分成词
words = text.split()
# 统计词频
word_counts = Counter(words)
# 获取排名和频率
ranks = range(1, len(word_counts) + 1)
frequencies = [count for word, count in word_counts.most_common()]
# 绘制排名-频率分布图
plt.figure(figsize=(10, 6))
plt.loglog(ranks, frequencies, marker="o")
plt.title("词频分布")
plt.xlabel("排名")
plt.ylabel("频率")
plt.show()
我们得到一个对数-对数图,显示了文本中每个单词排名的频率,遵循 Zipf 分布 -
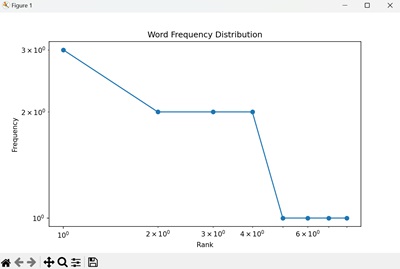
估算 Zipf 指数
在实际应用中,我们经常需要估算 Zipf 分布的指数参数。这可以通过各种统计技术来实现。一种简单的方法是将一条线拟合到秩与频率的对数-对数图上。
示例:估算指数
在下面的示例中,估算的指数接近实际值 (a = 2),证明了估算方法的准确性 -
import numpy as np
from scipy.stats import linregress
# 生成大量样本
a = 2
samples = np.random.zipf(a, size=1000)
# 统计每个秩的出现次数
unique, counts = np.unique(samples, return_counts=True)
# 在对数-对数图上执行线性回归
log_ranks = np.log(unique)
log_counts = np.log(counts)
slope, intercept, r_value, p_value, std_err = linregress(log_ranks, log_counts)
print("估计指数:", -slope)
输出结果如下:-
估计指数:0.8852106553815038
模拟真实场景
让我们使用 Zipf 分布模拟一个真实场景。假设我们要对某个热门新闻网站的访问量分布进行建模。
示例:网站访问量
我们可以从 Zipf 分布中生成大量样本,并分析不同页面的访问量分布 -
import matplotlib.pyplot as plt
import numpy as np
# 生成 Zipf 样本
a = 1.5
samples = np.random.zipf(a, size=10000)
# 统计每次页面访问的次数
unique, counts = np.unique(samples, return_counts=True)
# 绘制排序-频率分布
plt.figure(figsize=(10, 6))
plt.loglog(unique, counts, marker="o")
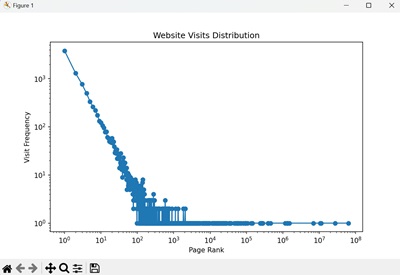
plt.title("网站访问量分布")
plt.xlabel("页面排名")
plt.ylabel("访问频率")
plt.show()
我们获得了一个对数-对数图,展示了网站访问量的分布,证明了 Zipf 分布的厚尾和幂律特性 -