NumPy - 计算多项式

在 NumPy 中计算多项式

在 NumPy 中计算多项式意味着计算多项式在特定点的值。您可以使用 NumPy 中的 numpy.polyval() 函数来实现这一点。

多项式由其系数定义，从最高次项开始，到常数项结束。该函数在给定 x 值处计算多项式，并且可以同时处理多个 x 值，并返回相应的结果。

numpy.polyval() 函数

numpy.polyval() 函数针对给定的 x 值(或值数组)计算多项式。它接受两个参数:多项式的系数和多项式求值的点。

多项式以其系数表示，从最高幂项开始，到常数项结束。

示例:在单点求多项式的值

考虑多项式 f(x) = 2x - 3x + 4。我们可以计算 x = 2 处的多项式 −

import numpy as np

# 定义多项式 2x - 3x + 4 的系数
coefficients = np.array([2, -3, 4])

# 使用 numpy.polyval 计算 x = 2 处的多项式
x_value = 2
result = np.polyval(coefficients, x_value)

print(f"x = {x_value} 处的多项式值: {result}")

计算 x = 2 处的多项式的结果为 −

x = 2 处的多项式值:6

计算多项式在多个点处

除了在单点处求多项式的值外，numpy.polyval() 函数还可以同时在多个点处求多项式的值。该函数接受一个包含 x 值的数组，并返回一个包含相应结果的数组。

示例

让我们在多个 x 值处求同一个多项式 f(x) = 2x - 3x + 4 的值 -

import numpy as np

# 定义多项式 2x - 3x + 4 的系数
coefficients = np.array([2, -3, 4])

# 定义要求值的 x 值
x_values = np.array([-1, 0, 1, 2])

# 使用 numpy.polyval 在多个点求多项式的值
results = np.polyval(coefficients, x_values)

print("多项式在 x = [-1, 0, 1, 2] 处的值:", results)

在给定点求多项式的结果如下所示 -

多项式在 x = [-1, 0, 1, 2] 处的值:[9 4 3 6]

用复数求多项式的值根

即使多项式有复数根或系数，numpy.polyval() 函数仍然可以正确计算该多项式。如果结果涉及复数运算，该函数将返回复数。

示例

考虑多项式 f(x) = (2 + 3i)x + (1 - 2i)x + (4 + i)。我们可以像下面这样在 x = 1 + i 处求该多项式的值 -

import numpy as np

# 用复数定义多项式的系数
coefficients_complex = np.array([2 + 3j, 1 - 2j, 4 + 1j])

# 定义要求值的 x 值
x_value_complex = 1 + 1j

# 使用 numpy.polyval 在 x = 1 + 1j 处求多项式的值
result_complex = np.polyval(coefficients_complex, x_value_complex)

print(f"Value of the complex polynomial at x = {x_value_complex}: {result_complex}")

对复系数多项式求值的结果是 −

Value of the complex polynomial at x = (1+1j): (1+4j)

曲线绘制的多项式求值

在曲线绘制中，通常使用在 x 值范围内求多项式的值，例如绘制多项式函数的图形时。可以通过将 x 值数组传递给 numpy.polyval() 函数并绘制结果值来实现。

示例:绘制多项式曲线

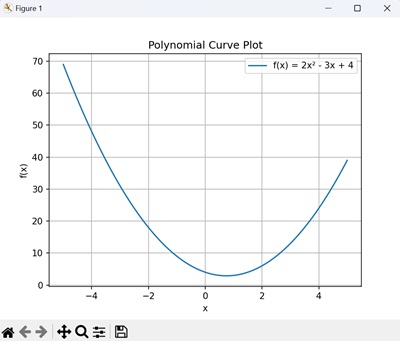
让我们在 x = -5 到 x = 5 − 的范围内绘制多项式 f(x) = 2x - 3x + 4。

import numpy as np
import matplotlib.pyplot as plt

# 定义多项式 2x - 3x + 4 的系数
coefficients = np.array([2, -3, 4])

# 定义 x 值的范围
x_values_plot = np.linspace(-5, 5, 100)

# 使用 numpy.polyval 计算 x 值处的多项式
y_values_plot = np.polyval(coefficients, x_values_plot)

# 绘制多项式曲线
plt.plot(x_values_plot, y_values_plot, label='f(x) = 2x - 3x + 4')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Polynomial Curve Plot')
plt.legend()
plt.grid(True)
plt.show()

显示的输出如下所示 -