NumPy - 逻辑分布
什么是逻辑分布?
逻辑分布是一种连续概率分布,用于建模增长和逻辑回归。
它由两个参数定义:位置参数(均值)和尺度参数 s。该分布与正态分布相似,但尾部更重,这意味着极值概率更高。
示例:逻辑斯蒂分布可以描述人口增长,其中增长率与现有数量和剩余增长量成正比。
逻辑斯蒂分布的概率密度函数 (PDF) 定义为 −
f(x; , s) = (e-(x-)/s) / (s * (1 + e-(x-)/s)2)
其中,
- :位置参数(平均值)。
- s:尺度参数(与标准偏差)。
- x: 随机变量的值。
- e: 欧拉常数(约为 2.71828)。
使用 NumPy 生成逻辑分布
NumPy 提供了 numpy.random.logistic() 函数来生成逻辑分布的样本。您可以指定位置参数 、尺度参数 s 以及生成样本的大小。
示例
在此示例中,我们从位置参数 =0 且尺度参数 s=1 的逻辑分布中生成 10 个随机样本 -
import numpy as np
# 从位置参数 =0 且尺度参数 s=1 的逻辑分布中生成 10 个随机样本
samples = np.random.logistic(loc=0, scale=1, size=10)
print("来自逻辑分布的随机样本:", sample)
以下是获得的输出 -
来自逻辑分布的随机样本:[-1.6473898 1.18698013 -0.24048488 -1.05235482 3.11858778 -1.40235809 0.8399973 -1.46670621 -3.14359949 -0.80023521]
可视化逻辑分布
可视化逻辑分布有助于更好地理解其特性。我们可以使用 Matplotlib 等库来创建直方图,以显示生成样本的分布。
示例
在下面的示例中,我们首先生成 1000 个随机逻辑分布样本,其中 =0 且 s=1。然后,我们创建一个直方图来可视化此分布 -
import numpy as np
import matplotlib.pyplot as plt
# 从逻辑分布中生成 1000 个随机样本,其中 =0 且 s=1
samples = np.random.logistic(loc=0, scale=1, size=1000)
# 创建一个直方图来可视化此分布
plt.hist(samples, bins=30, edgecolor='black', density=True)
plt.title('逻辑分布')
plt.xlabel('值')
plt.ylabel('频率')
plt.show()
直方图显示了逻辑分布中值的频率。条形表示每种可能结果的概率,形成逻辑分布特有的 S 形 -

逻辑分布的应用
逻辑分布在各个领域用于对具有极值的数据进行建模。以下是一些实际应用 -
- 机器学习: 使用逻辑回归建模二元结果。
- 经济学: 建模收入和财富的增长与分配。
- 统计学: 使用逻辑模型分析和预测结果。
生成累积逻辑分布
有时,我们对逻辑分布的累积分布函数 (CDF) 感兴趣,它给出了区间内发生最多 x 个事件(包括 x 个事件)的概率。
NumPy 没有内置逻辑分布 CDF 函数,但我们可以使用循环和 SciPy 库中的 scipy.stats.logistic.cdf() 函数来计算它。库。
示例
以下是在 NumPy 中生成累积逻辑分布的示例 -
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import logistic
# 定义位置和尺度参数
loc = 0
scale = 1
# 生成累积分布函数 (CDF) 值
x = np.linspace(-10, 10, 100)
cdf = logistic.cdf(x, loc=loc, scale=scale)
# 绘制累积分布函数 (CDF)
plt.plot(x, cdf, marker='o', linestyle='-', color='b')
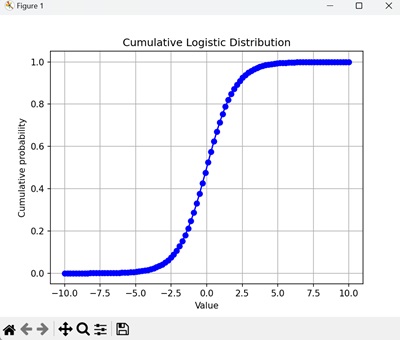
plt.title('累积逻辑斯蒂分布')
plt.xlabel('值')
plt.ylabel('累积概率')
plt.grid(True)
plt.show()
该图显示了逻辑斯蒂试验中达到并包含每个值的累积概率。 CDF 是一条平滑曲线,随着值的增加而增加到 1 -
逻辑斯蒂分布的性质
逻辑斯蒂分布有几个关键性质,例如 -
- 位置参数 (): 位置参数是分布的均值。
- 尺度参数 (s): 尺度参数与分布的标准差有关。
- 均值和方差: 逻辑斯蒂分布的均值为 ,方差为 (s22/3)。
- 偏度: 分布围绕均值对称,尾部比正态分布。
使用逻辑斯蒂分布进行假设检验
逻辑斯蒂分布常用于假设检验,尤其是在二元结果检验中。
一种常见的检验方法是逻辑斯蒂回归,它用于根据一个或多个预测变量对二元结果的概率进行建模。以下是使用 statsmodels 库的示例:
示例
在此示例中,我们用逻辑斯蒂回归模型拟合二元结果数据。摘要提供了模型的系数、标准误差和 p 值的信息 -
# Python 版本 3.11 import numpy as np import statsmodels.api as sm # 示例数据 X = np.array([0, 1, 2, 3, 4, 5]) y = np.array([0, 0, 0, 1, 1, 1]) # 向预测变量添加一个常量 X = sm.add_constant(X) # 拟合逻辑回归模型 model = sm.Logit(y, X) result = model.fit(method='lbfgs', maxiter=100, disp=0) # 打印模型摘要 print(result.summary())
得到的输出如下所示−
Logit Regression Results
==============================================================================
Dep. Variable: y No. Observations: 6
Model: Logit Df Residuals: 4
Method: MLE Df Model: 1
Date: Wed, 20 Nov 2024 Pseudo R-squ.: 1.000
Time: 12:29:27 Log-Likelihood: -5.7054e-05
converged: True LL-Null: -4.1589
Covariance Type: nonrobust LLR p-value: 0.003926
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -52.2706 668.240 -0.078 0.938 -1361.997 1257.456
x1 20.9332 265.301 0.079 0.937 -499.046 540.913
==============================================================================
Complete Separation: The results show that there iscomplete separation or perfect prediction.
In this case the Maximum Likelihood Estimator does not exist and the parameters
are not identified.
种子设定以确保可重复性
为了确保可重复性,您可以在生成逻辑分布之前设置特定的种子。这可以确保每次运行代码时都会生成相同的随机数序列。
示例
在此示例中,我们在生成逻辑分布的随机样本之前将种子设置为 42。种子确保每次运行代码时生成相同的样本序列 -
import numpy as np
# 设置种子以确保可重复性
np.random.seed(42)
# 从逻辑分布中生成 10 个随机样本,其中 =0 且 s=1
samples = np.random.logistic(loc=0, scale=1, size=10)
print("种子为 42 的随机样本:", sample)
以下是上述代码的输出 -
种子为 42 的随机样本:[-0.51278827 2.95957976 1.00476265 0.39987857 -1.68815492 -1.68833811-2.78603295 1.86756387 0.41011316 0.88604138]

