NumPy - 瑞利分布

什么是瑞利分布?

瑞利分布是一种连续概率分布，用于对二维平面中向量的幅值进行建模，其分量相互独立，且服从等方差正态分布。

它由尺度参数 (sigma) 定义。这种分布常用于信号处理和通信理论中，以对散射信号进行建模。

例如，瑞利分布可以描述风速分布，假设两个正交方向上的风速分量相互独立且呈正态分布。

瑞利分布的概率密度函数 (PDF) 定义为 −

当 x 为 0 时，f(x; ) = (x / 2) * exp(-x2 / (22))，否则为 0

其中:

• :尺度参数(与标准差相关)。
• x:矢量的幅度。
• exp:指数函数。

使用 NumPy 生成瑞利分布

NumPy 提供了 numpy.random.rayleigh() 函数来生成瑞利分布的样本。您可以指定尺度参数和生成样本的大小。

示例

在此示例中，我们从尺度参数 =1 的瑞利分布中生成 10 个随机样本 -

import numpy as np

# 从尺度参数 =1 的瑞利分布中生成 10 个随机样本
samples = np.random.rayleigh(scale=1, size=10)
print("来自瑞利分布的随机样本:", sample)

以下是获得的输出 -

来自瑞利分布的随机样本:[1.31998799 0.72631303 2.4544915 0.31195556 1.14244968 0.299947020.74889027 0.2239033 1.43290625 1.18894253]

可视化瑞利分布

可视化瑞利分布有助于更好地理解其特性。我们可以使用 Matplotlib 等库来创建直方图，以显示生成样本的分布。

示例

在下面的示例中，我们首先从 θ =1 的瑞利分布中生成 1000 个随机样本。然后我们创建一个直方图来可视化该分布 -

import numpy as np
import matplotlib.pyplot as plt

# 从瑞利分布中生成 1000 个随机样本，其中 =1
samples = np.random.rayleigh(scale=1, size=1000)

# 创建一个直方图来可视化该分布
plt.hist(samples, bins=30, edgecolor='black', density=True)
plt.title('瑞利分布')
plt.xlabel('幅度')
plt.ylabel('频率')
plt.show()

直方图显示了瑞利试验中向量幅度的频率。条形表示每种可能结果的概率，构成了瑞利分布的特征形状 -

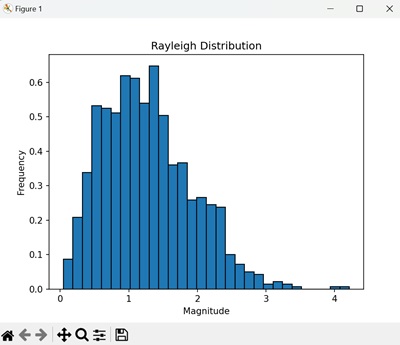
瑞利分布的应用

瑞利分布在各个领域都有应用，用于对高斯随机变量向量的幅值进行建模。以下是一些实际应用 -

• 信号处理: 对具有多条散射路径的信号包络进行建模。
• 雷达系统: 对具有随机散射的目标的接收信号强度进行建模。
• 通信理论: 对受多径衰落影响的信号幅度进行建模。

生成累积瑞利分布

有时，我们对瑞利分布的累积分布函数 (CDF) 感兴趣，它给出了在间隔内发生最多 x 个事件(包括 x 个事件)的概率。

NumPy 没有内置瑞利分布 CDF 函数，但我们可以使用循环和 SciPy 库中的 scipy.stats.rayleigh.cdf() 函数来计算它。库。

示例

以下是在 NumPy 中生成累积瑞利分布的示例 -

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import rayleigh

# 定义尺度参数
sigma = 1

# 生成累积分布函数 (CDF) 值
x = np.linspace(0, 5, 100)
cdf = rayleigh.cdf(x, scale=sigma)

# 绘制 CDF 值
plt.plot(x, cdf, marker='o', linestyle='-', color='b')
plt.title('累积瑞利分布')
plt.xlabel('震级')
plt.ylabel('累积概率')
plt.grid(True)
plt.show()

该图显示了瑞利试验中达到并包含每个震级的累积概率。 CDF 是一条平滑曲线，随着幅值的增加而增加到 1 -

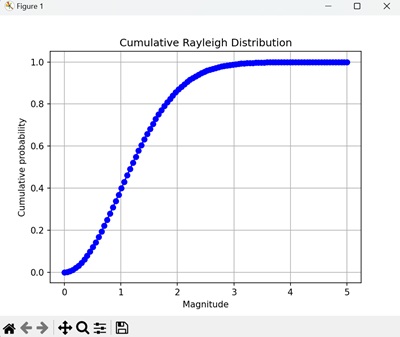
瑞利分布的性质

瑞利分布有几个关键性质，例如 -

• 尺度参数 ():尺度参数与底层高斯随机变量的标准差有关。
• 均值和方差:瑞利分布的均值为 (/2)，方差为 (2-/2)²。
• 偏度:分布向右偏斜，尾部较长。

使用瑞利分布进行假设检验

瑞利分布常用于假设检验，尤其是在向量幅值的检验中。

瑞利检验是一种常见的检验方法，用于确定观测幅值与预期幅值是否存在显著差异。以下是使用 scipy.stats.rayleigh() 函数的示例:

示例

在此示例中，我们执行瑞利检验来确定观测幅值 (1.5) 是否与预期幅值 (=1) 存在显著差异。 p值表示假设零假设成立，获得至少与观测结果同样极端的结果的概率 -

from scipy.stats import rayleigh

# 观测震级
observed_magnitude = 1.5

# 预期尺度参数 ()
expected_scale = 1

# 执行瑞利检验
p_value = rayleigh.sf(observed_magnitude, scale=expected_scale)
print("瑞利检验的P值:", p_value)

输出结果如下所示 -

瑞利检验的P值:0.32465246735834974

种子可重复性

为了确保可重复性，您可以在生成瑞利分布之前设置特定的种子。这样可以确保每次运行代码时都生成相同的随机数序列。

示例

通过设置种子，可以确保每次执行代码时随机生成的结果都相同，如下例所示 -

import numpy as np

# 设置种子以确保可重复性
np.random.seed(42)

# 从瑞利分布中生成 10 个随机样本，其中 =1
samples = np.random.rayleigh(scale=1, size=10)
print("种子为 42 的随机样本:", sample)

生成的结果如下 -

种子为 42 的随机样本: [0.96878077 2.45361832 1.62280356 1.35125316 0.58245149 0.58240242
 0.34594441 2.00560757 1.35578918 1.56923552]