NumPy - 均匀分布
什么是均匀分布?
均匀分布是一种概率分布,其中所有结果的概率均相等。这意味着任何给定结果的概率在可能结果范围内都是恒定的。
均匀分布可以是连续的,也可以是离散的。在连续均匀分布中,结果可以取指定范围内的任意值。相反,离散均匀分布的可能结果集是有限的。
使用 NumPy 实现均匀分布
NumPy 提供了 numpy.random.uniform() 函数来从连续均匀分布中生成样本。此函数允许您指定生成样本的范围和大小。
示例
在此示例中,我们从 0 到 1 之间的均匀分布中生成 10 个随机样本 -
import numpy as np
# 从 0 到 1 之间的均匀分布中生成 10 个随机样本
samples = np.random.uniform(0, 1, 10)
print("均匀分布的随机样本:", sample)
以下是获得的输出 -
均匀分布的随机样本:[0.70748409 0.45654756 0.73426382 0.15580835 0.70294526 0.12503631 0.40303738 0.9862709 0.4923119 0.44059809]
可视化均匀分布
可视化均匀分布有助于更好地理解其特性。我们可以使用 Matplotlib 等库来创建直方图,以显示生成样本的分布情况。
示例
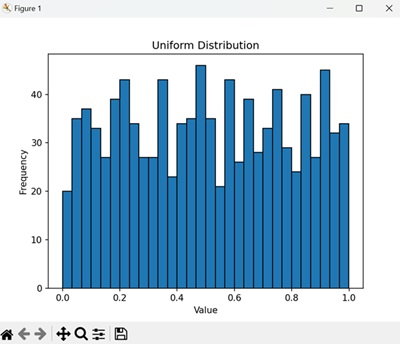
在以下示例中,我们将从 0 到 1 之间的均匀分布中生成 1000 个随机样本,然后创建一个直方图来可视化此分布 -
import numpy as np
import matplotlib.pyplot as plt
# 从 0 到 1 之间的均匀分布中生成 1000 个随机样本
samples = np.random.uniform(0, 1, 1000)
# 创建直方图来可视化分布
plt.hist(samples, bins=30, edgecolor='black')
plt.title('Uniform分布')
plt.xlabel('值')
plt.ylabel('频率')
plt.show()
直方图显示样本在0和1之间均匀分布,每个区间的频率大致相等 -
均匀分布的应用
均匀分布应用于各个领域,包括计算机模拟、蒙特卡洛方法和随机抽样。以下是一些实际应用 -
- 模拟:均匀分布用于模拟模型中每个结果发生概率相同的随机事件。
- 随机抽样:均匀分布用于从总体中生成随机样本进行统计分析。
- 蒙特卡洛方法:均匀分布用于蒙特卡洛模拟,生成用于估计复积分和解决物理和金融问题的随机数。
生成离散均匀分布
NumPy 还允许使用 numpy.random.randint() 函数从离散均匀分布生成样本。此函数生成指定范围内的随机整数。
示例
在此示例中,我们生成 10 个介于 1 和 10 之间的随机整数(含 1 和 10)-
import numpy as np
# 生成 10 个介于 1 和 10 之间的随机整数
samples = np.random.randint(1, 11, 10)
print("离散均匀分布的随机样本:", sample)
以下是得到的输出 -
离散均匀分布的随机样本:[ 7 3 9 10 9 4 8 4 1 7]
均匀分布的性质分布
均匀分布有几个关键属性,如下所示:
- 恒定概率密度:在连续均匀分布中,概率密度函数 (PDF) 在指定范围内保持恒定。
- 等似然性:范围内所有结果的概率均等。
- 均值和方差:对于 a 和 b 之间的连续均匀分布,均值为 (a + b) / 2,方差为 ((b - a)2) / 12。
计算平均值和方差
您可以使用简单的公式计算均匀分布的平均值和方差。让我们看看如何计算 a 和 b 之间均匀分布的均值和方差。
示例
本例计算了 0 和 1 之间均匀分布的均值和方差 -
import numpy as np
# 定义均匀分布的范围
a = 0
b = 1
# 计算均值和方差
均值 = (a + b) / 2
方差 = ((b - a) ** 2) / 12
print("均值:", 均值)
print("方差:", 方差)
以下是得到的输出 -
均值: 0.5 方差:0.08333333333333333
多维数组中的均匀分布
NumPy 也可以为多维数组生成均匀分布。以下是示例:
示例
本例生成一个 3x3 的数组,其中包含 0 到 1 之间均匀分布的随机样本 -
import numpy as np
# 生成一个 3x3 的数组,其中包含 0 到 1 之间的均匀分布的随机样本
samples = np.random.uniform(0, 1, (3, 3))
print("3x3 的均匀分布随机样本数组:", sample)
输出结果如下 -
3x3 的均匀分布随机样本数组: [[0.18528116 0.65725829 0.06597822] [0.73183704 0.05931206 0.65555952] [0.92479579 0.89807463 0.02624335]]
种子设定以确保可重复性
为确保可重复性,您可以在生成均匀分布之前设置特定的种子。这样可以确保每次运行代码时都会生成相同的随机数序列。
示例
通过设置种子,可以确保每次执行代码时随机生成的结果都相同,如下例所示 -
import numpy as np
# 设置种子以确保可重复性
np.random.seed(42)
# 从 0 到 1 之间的均匀分布中生成 10 个随机样本
samples = np.random.uniform(0, 1, 10)
print("种子为 42 的随机样本:", sample)
以下是获得的输出 -
种子为 42 的随机样本:[0.37454012 0.95071431 0.73199394 0.59865848 0.15601864 0.15599452 0.05808361 0.86617615 0.60111501 0.70807258]

