NumPy - 帕累托分布

什么是帕累托分布?

帕累托分布是一种连续概率分布，用于模拟财富、收入或其他资源的分布，其中一小部分人口控制着很大一部分的总体。

它由两个参数定义:形状参数和尺度参数 x_m。该分布以其"80/20 规则"而闻名，即大约 80% 的结果来自 20% 的原因。

示例:帕累托分布可以模拟人口中的财富分配，其中少数人掌握着大部分财富。

帕累托分布的概率密度函数 (PDF) 为 −

f(x; , xm) = ( * xm) / x+1，其中 x = xm

其中:

• :形状参数，决定分布尾部的陡度。
• xm:尺度参数，表示分布的最小值(也称为"阈值")。
• x:表示我们感兴趣的值的随机变量。
• + 1:随机变量的指数，显示分布的厚尾特性。

帕累托分布常用于模拟"富者愈富"现象，即某个值的概率随着其增加而迅速下降。

NumPy 中的帕累托分布

NumPy 提供了一个内置函数 numpy.random.pareto()，用于根据帕累托分布生成随机样本。你需要指定形状参数和尺度参数 xm。该函数将根据帕累托分布生成随机值。

示例

在此示例中，我们从形状参数 () 为 2、尺度参数 (xm) 为 1 的帕累托分布中生成 10 个随机样本。由于帕累托分布的定义是大于或等于 xm 的值，因此我们加 1 以将分布从 1 开始 -

import numpy as np

# 从形状参数 =2、尺度参数 xm =1 的帕累托分布中生成 10 个随机样本
samples = np.random.pareto(a=2, size=10) + 1 # xm = 1，我们加 1 以移动分布
print("来自帕累托分布的随机样本:", sample)

以下是获得的输出 -

来自帕累托分布的随机样本:[11.21752644 1.19133192 1.13107575 1.00672706 1.77411845 1.29541783
5.99272696 1.62119397 1.08409404 1.25025651]

可视化帕累托分布

可视化是理解分布特征的重要工具。我们可以通过使用 Matplotlib 创建直方图来可视化帕累托分布。

示例

在下面的示例中，我们首先从帕累托分布中生成 1000 个随机样本。然后，我们创建样本的直方图来可视化此分布 -

import numpy as np
import matplotlib.pyplot as plt

# 从帕累托分布中生成 1000 个随机样本
samples = np.random.pareto(a=2, size=1000) + 1

# 绘制样本的直方图
plt.hist(samples, bins=30, density=True, edgecolor='black')
plt.title('帕累托分布')
plt.xlabel('值')
plt.ylabel('概率密度')
plt.grid(True)
plt.show()

直方图显示了生成值的概率密度。正如预期，该分布具有"厚尾"，这意味着少数较大的值对总概率有显著的贡献。随着值的增加，分布迅速衰减 -

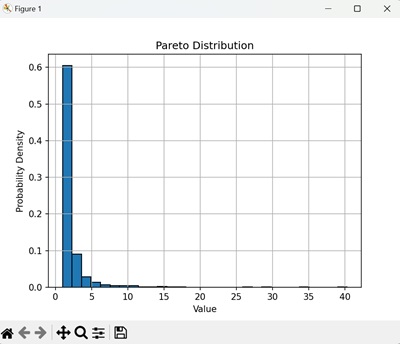
帕累托分布的参数

帕累托分布的两个参数和xm在分布的形成过程中起着重要作用。让我们来分析一下每个参数如何影响分布 -

• 形状参数 ():形状参数控制分布尾部的陡度。随着的增加，尾部变得更陡，分布的"厚尾"程度降低。越小，分布的尾部越厚，极值也越多。
• 尺度参数 (xm):尺度参数设置分布的最小值。较高的 xm 会使分布向右移动，这意味着随机样本只会取大于或等于此阈值的值。

帕累托分布的应用

帕累托分布在建模和数据分析中有许多实际应用 -

• 经济学:帕累托分布通常用于模拟收入分配、财富分配以及其他一小部分人口控制大量财富的经济现象。
• 网络流量:它可用于模拟互联网流量，其中少数用户生成大部分数据。
• 保险:帕累托分布应用于风险建模，尤其是在自然灾害等领域，这些领域虽然损失惨重，但损失却不小。
• 工程:它用于模拟工程中的组件故障，其中少数组件经常发生故障，而其余组件的使用寿命很长。

帕累托分布的统计特性

与其他分布一样，帕累托分布也具有一些有趣的统计特性 -

• 均值:当 > 1时，帕累托分布的均值为 * xm / ( - 1)。如果 1，则均值不确定，因为该分布具有厚尾。
• 方差:当 > 2时，帕累托分布的方差为 * xm / ( ( - 1) * ( - 2))。如果 2 为 2，则由于尾部较厚，方差为无穷大。
• 偏度:帕累托分布向右偏斜，这意味着它在正侧有一个长尾。

使用自定义参数生成帕累托分布

您可以修改形状和尺度参数，以生成更能反映数据的帕累托分布。

示例

以下示例设置 =3 和 xm=2 来生成帕累托分布 -

import numpy as np
import matplotlib.pyplot as plt

# 生成 1000 个随机样本，其中 =3 且 xm=2
samples = np.random.pareto(a=3, size=1000) + 2

# 绘制样本直方图
plt.hist(samples, bins=30, density=True, edgecolor='black')
plt.title('=3 且 xm=2 的帕累托分布')
plt.xlabel('值')
plt.ylabel('概率密度')
plt.grid(True)
plt.show()

此图显示的分布尾部比=2 且 xm=1 的分布略轻 -

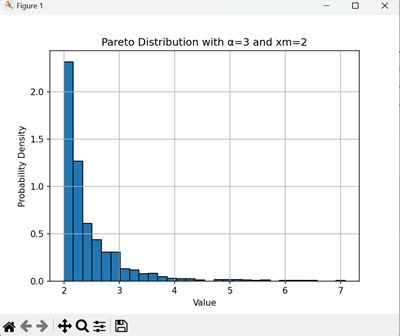
种子设定以提高可重复性

为了提高可重复性，设置随机种子非常重要。这样可以确保每次运行代码时，都能获得相同的随机数集。

示例

通过设置种子，可以确保每次执行代码时随机生成的结果都相同，如下例所示 -

import numpy as np

# 设置种子以确保可重复性
np.random.seed(42)

# 生成 10 个随机样本，其中 =2 且 xm=1
samples = np.random.pareto(a=2, size=10) + 1
print("使用种子从帕累托分布中随机抽样:", sample)

生成的结果如下 -

使用种子从帕累托分布中随机抽样，其中:[1.26444595 4.50442711 1.93164669 1.57849408 1.08851288 1.08849733
 1.03037147 2.73358909 1.58334718 1.85081305]